Advance Data Structures and Algorithm Analysis

约 3022 个字 66 行代码 预计阅读时间 11 分钟

AVL tree(平衡二叉树)

AVL 数的想法是强制要求每次插入，删除之后都保证树的绝对平衡

AVL 数的递归定义

一颗空的树或它的左右两个子树的高度差的绝对值不超过1是AVL树，同时它的左右两个子树也是AVL树（从下往上看，不要从上往下看）

• 平衡因子(Balence factor) 简称 \(bf\),计算公式为

$$ bf = height_{left}-height_{right} $$

在AVL tree 中，\(bf\) 只能为 -1,0,1 三种情况之一

AVL tree 可以解决当顺序数据被插入到普通二叉搜索树的过程中，二叉搜素树会退化为链表的过程

不同类型的插入

LL型-右旋

在某结点的左结点(L)的左子树(L)上做了插入元素的操作导致失衡，我们称这种情况为左左型，应该进行右旋转

• A 向右旋转成为 B 的 右 child
• B的右子树成为A的左子树

Warning

需要注意的是，在这里，节点A的 \(bf\) 值只能是1，如果是0，说明左右树高相等，再插入也是AVL树，如果是-1，说明左边比右边矮，左边再长高1，也不会导致失衡

RR型-左旋

在某结点的 右结点(R)的 右子树(R)上做了插入元素的操作，我们称这种情况为 右右型 ，我们应该进行左旋转。

• A 向左旋转成为B的左child
• B 的左子树 成为 A 的右子树

Warning

节点A的 \(bf\) 值也是确定的

Note

总的来说，对于LL和RR型，我们解决失衡的方式是

对于LL，左结点当根

对于RR，右节点当根

LR 型-左右旋

在某结点的 左结点（L） 的 右子树（R） 上做了插入元素的操作导致失衡，我们称这种情况为 左右型 ，我们应该进行左右旋。

对于左右型，如果只进行单旋，不会解决问题

• 需要进行两次旋转(左右旋)
  • 第一次（左旋）: B左旋，成为C的左结点，C的左子树成为B的右子树
  • 第二次（右旋）: A右旋，成为C的右节点，C的右子树成为A的左子树

一个例子

RL 型-右左旋转

在某节点的在结点T的 右结点（R） 的 左子树（L） 上做了插入元素的操作，我们称这种情况为 右左型 ，我们应该进行右左旋。

同样，单旋对于RL型也没有用

• 需要进行两次旋转(右左旋)
  • 第一次（右旋）: B右旋，称为C的右结点，C的右子树成为B的左子树
  • 第二次（左旋）: A左旋，成为C的左节点，C的左子树成为A的右子树

总结

总的来说，对于LR和RL型，我们解决失衡的方式是

对于LR，左结点的右 child 当根

对于RL，右节点的左child 当根

Tip

如果一次插入最多只会导致插入路径上的一连串的结点失衡，我们只需要解决找到的第一个（最靠下的）失衡结点，将其解决，上面的结点自然也恢复到正常的平衡因子,所以，对于每次插入，我们至多只需要进行一次 rotation 就可以解决冲突了 但是对于删除，最坏的情况却要旋转 \(\log(n)\) 次

旋转前后，结点之间的相对位置不变，亦即左边的结点仍然在左边，右边的结点仍然在右边

AVL 树的搜索、插入和删除操作的时间复杂度为 \(O(\log n)\)

Splay tree(伸展树)

吴一航学长的ADS讲义

Splay 树的想法一方面来源于希望可以不像 AVL 那样保持严格的平衡约束，但也能保证某种层面（均摊）的对数时间复杂度，另一方面 Splay 树在访问（特别注意访问包括搜索、插入和删除）时都需要将元素移动到根结点，这非常符合程序局部性的要求，即刚刚访问的数据很有可能再次被访问，因此在实现缓存和垃圾收集算法中有一定的应用。

Splay 树并不在乎二叉树是否时刻都平衡，而是通过在每次操作时加上Splay操作，即通过一系列旋转将我们访问的结点移动到根结点

Note

Any M consecutive tree operations starting from an empty tree take at most \(O(M \log N)\) time.

Splay tree 希望从一棵空树开始连续的M个操作是 \(O(M \log N)\) 的

我们有两种旋转方式

naive的方式:

不断地把访问的结点与其父节点更换父子方式，即不断使用单旋一直转到根节点的位置，但是这种方法虽然满足了将访问的结点移动到根的需求，其路径上的结点却被移动到了很深的位置，这种方式不满足我们对于复杂度的要求

下面是合理的旋转方式:

对于任何不是根结点的结点 X ,我们关心它的 parent 节点 P 和它的 grandparent 结点 G:

• case 1: 如果 P 已经是根，直接旋转交换 P 和 X ，这与普通方法没什么区别
• case 2: 如果 P 并不是根，又分为两种情况
  • Zig-zag(之字型): 双旋,使得X成为树根(不一定是树的根，是XPG子树的树根)，这种情况与普通方法是一样的，与 AVL 树的 RL 和 LR 型也是一样的
  • Zig-zig(同侧型): 单旋，其实叫做单旋，实际上也是转两次，应该是为了和 AVL 树不一样才这么叫。 Zig-zig 的方法才是是与naive的方法不一样的地方,普通方法先交换了 X 和 P 的位置，再交换 X 和 G 的位置; Zig-zig 的操作方法是先交换 P 和 G ，再交换 X 和 P，相当于 X 直接跨了两步

insert 1 to 7 and then find 1

编程实践-Find root of AVL tree

For each case, the first line contains a positive integer \(N\) which is the total number of keys to be inserted. Then \(N\) distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

output the root of AVL treeeeeeeeeeeeeee!

pseudo code

Define structure Node:
data: integer
left: pointer to Node (initially NULL)
right: pointer to Node (initially NULL)
height: integer (initially 0)

Define height(root):
    If root is NULL:
        Return -1
    Else:
        Return root.height

Define LL_rotation(root):
    new_root = root.left
    root.left = new_root.right
    new_root.right = root
    Update root.height
    Update new_root.height 
    Return new_root

Define RR_rotation(root):
    new_root = root.right
    root.right = new_root.left
    new_root.left = root
    Update root.height
    Update new_root.height 
    Return new_root

Define LR_rotation(root):
    root.left = RR_rotation(root.left)
    Return LL_rotation(root)

Define RL_rotation(root):
    root.right = LL_rotation(root.right)
    Return RR_rotation(root)

Define insert(root, x):
    If root is NULL:
        Create a new node with data x
        Set left and right child to NULL
        Set height to 0
        Return the new node
    Else if x < root.data:
        Recursively insert x into the left subtree
        If height difference between left and right subtree is 2:
            If x < root.left.data:
                Perform LL_rotation on root
            Else:
                Perform LR_rotation on root
    Else if x > root.data:
        Recursively insert x into the right subtree
        If height difference between right and left subtree is 2:
            If x > root.right.data:
                Perform RR_rotation on root
            Else:
                Perform RL_rotation on root
    Update root.height = max(height(root.left), height(root.right)) + 1
    Return root

Main function:
    Read integer N (number of nodes to be inserted)
    Initialize root as NULL
    For each node:
        Read integer x
        Insert x into the AVL tree (root = insert(root, x))
    Output the data of the root node

Amortized Analysis(摊还分析)

吴一航学长的ADS讲义

摊还分析的想法来源于我们希望估计一种数据结构经过一系列操作的平均花费时间。然而，平均时间 非常难计算，因为每一步都有非常多的选择，连续 m 个操作，可能的操作路径是指数级别的。并且有 时候平均涉及概率分布等，但我们并不知道确切的分布，因此比较难以计算。 一种最简单的估计方法就是用最差情况分析作为平均情况的上界，例如 Splay 树，每个操作最差都是 \(O(n)\)（n 为树中结点个数）的，因此平均不会比最差情况差，所以也是 \(O(n)\) 的。然而这样的估计显然 是放得太宽了，我们对这个复杂度是非常不满意的，因此我们需要进行摊还分析。事实上，在最差情况 的分析中，我们忽略了一件事情，就是有的序列是不可能出现的，例如直接在空的树上用 \(O(n)\) 时间删 除，摊还分析则是希望排除掉最差情况分析中把所有不管可能不可能的情况，最差的路径挑出来的这 种无脑行为，转而分析所有可能的从空结构开始的操作路径中，最差的平均时间，那么这一时间一定比 最差情况分析好，因为排除掉了一些不可能出现的所谓最差序列，但又会大于等于平均时间，因为取的 是所有可能序列中最差的那一种。因此当我们算出摊还分析的时间复杂度，那么它也一定是平均时间 的上界，同时这个上界会比最差情况分析好.

总的来说，我们希望分析 Average 的情况是比较困难的，分析 worst 的情况是比较粗糙的，所以我们使用摊还分析，通过"劫富济贫"(截长补短),将最坏的情况削弱，同时又是平均情况的上界，只要这种情况是满足条件的，我们就可以用它来证明。

准备工作

\[\hat{c}_i=c_i+\Delta_i\]

其中 \(\hat{c}_i\) 是第i次操作的摊还代价，\(c_i\) 是第i次操作的实际代价，\(\Delta_i\) 是第i次操作的是截的长（负值），或者补的短（正值）

我们还需要满足：

\[\sum_{i=1}^{n}\Delta_i \geqslant 0\]

所以：

\[\sum_{i=1}^{n}\hat{c}_i \geqslant \sum_{i=1}^{n}c_i\]

但是在面对Splay tree的操作，我们并不能每一次都很好的定义一种 \(\Delta_i\),所以我们需要用到势能函数，来构造首尾可以相消的项

\[\Delta_i=\Phi(D_n)-\Phi(D_{n-1})\]

这样，所有的成本

\[\sum_{i=1}^{n}\hat{c}_i = \sum_{i=1}^{n}c_i+\Phi(D_n)-\Phi(D_{0})\]

证明Splay tree每个操作的复杂度

我们定义势能函数 \(\Phi(T)\) 为

\[\Phi(T)=\sum_{x\in T}Rank(x)\]

其中 \(Rank(x)=\log S(x)\)

即以\(x\)为根的子树的结点数的对数，包括\(x\)本身

对于Zig操作,有一次旋转，real cost = 1

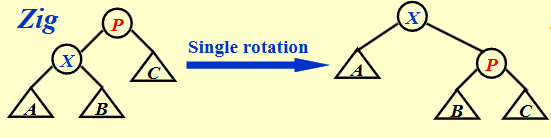
在放缩的过程中，我们保留\(X\) $$ \hat{c}_i = 1 + R_2(X) - R_1(X) \ + R_2(P) - R_1(P) \ \leqslant 1 + R_2(X) - R_1(X) $$ 这是很自然的，因为\(R_2(P) - R_1(P) \leqslant 0\)

对于Zig-zag操作，有两次旋转，real cost = 2

\[ \hat{c}_i = 2 + R_2(X) - R_1(X) \\ + R_2(P) - R_1(P) \\ + R_2(G) - R_1(G) \\ \leqslant 2 (R_2(X) - R_1(X)) \]

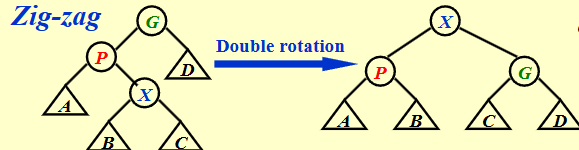
在这里，\(R_2(X)=R_1(G),R_1(P)>R_1(X)\) 所以，只需要考虑\(R_2(P) + R_2(G)+2\)为什么小于等于\(2R_2(X)\),对于旋转后的树，我们有

\[ \begin{align*} S(P) + S(G) + 1 &= S(X) \\ \log S(P) + \log S(G) + 2 &= \log 4S(P)S(G) \leqslant \log(S(P)+S(G))^2 \\ &= 2\log (S(X)-1) \leqslant 2R_2(X) \end{align*} \]

对于Zig-zig操作，有两次旋转，real cost = 2

\[ \hat{c}_i = 2 + R_2(X) - R_1(X) \\ + R_2(P) - R_1(P) \\ + R_2(G) - R_1(G) \\ \leqslant 3 (R_2(X) - R_1(X)) \]

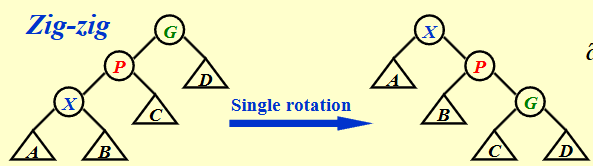
这种情况就稍难一点，首先我们仍然把\(R_2(X)=R_1(G)\),然后加上再减去\(R_1(X)\),此时式子变成

\[ \hat{c}_i = 2 + R_1(X) - R_1(X) \\ + R_2(P) - R_1(P) \\ + R_2(G) - R_1(X) \\ \leqslant 3 (R_2(X) - R_1(X)) \]

再有\(R_1(P) > R_1(X),R_2(P)<R_2(X)\) 那么就剩下\(R_1(X) + R_2(G) + 2 \leqslant 2R_2(X)\) 类似的，我们有

\[ \begin{align*} S_1(X) + S_2(G) + 1 &= S_2(X) \\ \log S_1(X) + \log S_2(G) + 2 &= \log 4S_1(X)S_2(G) \leqslant \log(S_1(X)+S_2(G))^2 \\ &= 2\log (S_2(X)-1) \leqslant 2R_2(X) \end{align*} \]

其实，这也是有迹可循的，主要想法就是用不等式的时候，左边两棵树没有互相包含的关系

总的来说，每次操作的 amortized cost 最多不超过 \(3 (R_2(X) - R_1(X))+1=O(\log N)\)

M次操作的总代价为 \(O(M\log N)\)

还没完，我们仍然需要证明，当初始势能不为0时，我们的摊还代价是正确的，其实即使不为0，我们可以确定其初始势能是有界的一个数

\[ \sum_{i=1}^{n}\hat{c}_i = \sum_{i=1}^{n}c_i+\Phi(D_n)-\Phi(D_{0}) \]

则平均摊还代价为

\[ \frac{\sum_{i=1}^{n}\hat{c}_i}{n} = \frac{\sum_{i=1}^{n}c_i}{n}+\frac{\Phi(D_n)}{n}-\frac{\Phi(D_{0})}{n} \]

当n趋近于无穷大时，尾项自然就去掉了，所以我们的摊还代价仍然大于等于实际代价，是合理的