红黑树与B+树¶

约 3903 个字 11 行代码预计阅读时间 14 分钟

我讨厌黑叔叔

红黑树不想像AVl树一样通过定义平衡因子，每次操作之后检查是否平衡，通过旋转来保持平衡，而是放松这一简单粗暴的想法，通过给结点染色，从而定义另一种平衡

红黑树的定义

一棵红黑树是满足以下性质的二叉搜索树

每个结点要么是红色，要么是黑色
根结点是黑色
每个叶结点（NIL结点，空结点）是黑色
如果一个结点是红色，那么它的两个子结点都是黑色
对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

需要注意的是，对于一个没有左子结点的结点，我们认为其子结点是NIL结点，是黑色的

我们称 NIL 为外部结点，其余有键值的结点为内部结点。
从某个结点 X 出发到达一个叶子结点（NIL）的任意一条简单路径上的黑色结点个数（不含 X 本身）称为 X 的黑高，记为 bh(X)。根据定义第五条，这一定义是合理的，因为从 X 出发到达一个叶子结点的任意一条简单路径上的黑色结点个数相同。除此之外，我们定义整棵红黑树的黑高为其根结点的黑高。

一棵有 $n$ 个内部结点的红黑树的高度至多为 $2 \log (n + 1)$。

吴一航学长的ADS讲义

如果我们舍去全部的红色结点，剩下的树的结点个数一定大于等于高度为 $bh(root)$ 的完全平衡二叉树的结点个数，因为删掉红色结点后可能不是二叉，这就是证明的第一个步骤：证明以 $X$ 为root结点的子树至少有 $2^{bh(x)} − 1$ 个内部结点。而根据第四条，任何路径上黑色结点必定占到至少一半的数量，因为红色不能是父子关系，所以有了证明的第二步，树高最多为黑高 $2$ 倍。

具体证明第一步，我们可以使用数学归纳法,对树的高度$h(x)$进行归纳

Proof

\[ For \enspace any \enspace node \enspace x, sizeof(x) \geqslant 2^{bh(x)} – 1.\\ Prove \enspace by \enspace induction.\\ If \enspace h(x) = 0, x \enspace is \enspace NULL\\ sizeof(x) = 2^0 – 1 = 0\\ Suppose \enspace it \enspace is \enspace true \enspace for \enspace all \enspace x \enspace with \enspace h(x) \leqslant k.\\ For \enspace x \enspace with \enspace h(x) = k + 1, \\ bh(child) = bh(x) \enspace or \enspace bh(x) – 1 \\ Since \enspace h(child) < k,\\ sizeof(child) \geqslant 2^{bh(child)} – 1 \geqslant 2^{bh(x)-1}– 1 \\ Hence \enspace sizeof(x) = 1 + 2sizeof(child) \geqslant 2^{bh(x)} – 1 \]

这样就得到了黑高的bound，再用第二步就得到了整个树高的上界了

Question

证明：在一棵红黑树中，从某结点 X 到其后代叶结点的所有简单路径中，最长的一条路径的长度至多是最短一条的 2 倍

最短路是全黑路，最长路是黑红相间的，而所有简单路径黑色结点个数一样，故而可以证明

对于搜索操作，红黑树的时间复杂度是 $O(\log n)$ 的,对于插入和删除，其情况就会更加复杂一些

红黑树的插入¶

向红黑树中插入结点时,有可能会破坏树的平衡性质,插入时需要将该结点初始颜色设置为红色，因为如果是黑色，那么其性质5一定会被破坏，接下来我们讨论每一种可能的情况

插入在黑结点下面¶

最简单的情况，没有破坏任何性质，不需要做任何调整

插入空树中¶

破坏了性质2，但是处理方法也很简单，直接将其染色成黑色即可

插入到红色结点的子节点中¶

此时唯一被违反的就是定义第四条，为了恢复，我们的想法是，在不影响性质5(以及其它性质)的前提下，通过一系列的染色和旋转使得没有父子都是红色,主要分为以下3种情况

X 有红叔叔¶

X 的叔叔（即父亲的兄弟）是红色的，X 无论左右孩子都是该情况

wyy有话说

这里所有结点都带子树，一方面至少有 NIL 结点，另一方面这可以不仅仅表示刚刚插入的情况，也可以表示经过几次调整后还在被这种情况困扰，因此更具一般性。注意 G 一定是黑色，因为 P 是红色，插入前它们就在红黑树中，因此不可能违背定义第四条

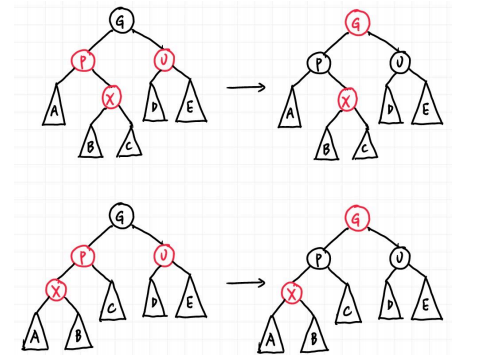
我们的想法是将X的红色甩掉，此时它的父亲和叔叔都是红色了，自然只能求助于祖父，但是我们不能直接交换它们的颜色(如果祖父是红色而叔叔父亲是红色，也不满足条件)，所以我们的方案将X的祖父染红，将X的父亲和叔叔染成黑色,(可以理解为将祖父的黑色分配给父亲和叔叔)此时不影响黑高的性质，但是并不代表问题已经解决了，因为曾祖父仍然可能是红色，但是至少问题网上推进了。如果一直推给根节点，根节点染黑即可，否则就是接下来的两种情况

X的叔叔是黑色的¶

情况2：X 的叔叔（即父亲的兄弟）是黑色的，且 X 是右孩子
情况3：X 的叔叔（即父亲的兄弟）是黑色的，且 X 是左孩子

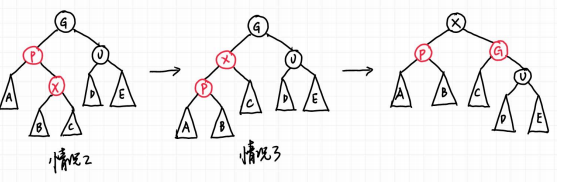
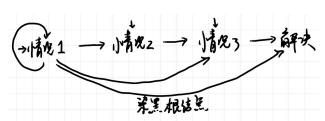
情况2和情况3之间是存在互相转换的(由图可知)，解决方案与AVL tree也是一致的，通过判断红色是LR还是LL来进行旋转，旋转完之后，重新染色，第一层是黑，第二层是红即可

Note

在以上的分析中，我们只考虑了X插入在左子树的情况，对于右子树的情况，实际上是完全对称的，对于情况一，仍然求助于祖父，对于情况二和情况三，则考虑RL和RR的情况,最后的染色也是一样的

吴一航学长的ADS讲义

如果插入后直接落入情况三，只需要一次旋转染色即可解决，直接落入情况二，一次旋转进入情况三，再一次旋转染色即可解决，但如果落入情况一，一次调整后可能还在情况一，可能直到最后都是通过情况一加上染黑根结点解决，也可能几次调整后进入情况二或三后解决。根据这一流程我们知道，红黑树插入最多可能的旋转次数为 2（因为只有情况 2 和 3 会要旋转进入情况 2 后 1 次旋转必定进入情况 3，进入情况 3 后 1 次旋转必定解决），然后 更改颜色最多是 $O(\log n)$ 次，因为进入情况 2 或 3 只需要一次染色，在情况 1 最差也是每两层染一次色，而我们已经证明红黑树的最大高度是$O(\log n)$的。因此插入操作包括$O(\log n)$的搜索时间，加常数的旋转，加$O(\log n)$的染色，因此还是$O(\log n)$的时间复杂度

一棵有 n 个内部结点的红黑树插入一个结点的时间复杂度为 $O(\log n)$。

Question

考虑从空树开始连续插入 $n(n > 1)$ 个结点得到一棵红黑树（每一步插入都要保证红黑树性质），试问这棵树一定会有红色结点吗？若是，请给出清晰的证明；若不是，请举出反例。

一定会，可以使用数学归纳法证明：n = 2 时显然正确，根下面插入的结点一定是红色且无需调整；此后如果不需要调整，因为我们插入的是红色结点，因此红色结点只可能变多；如果需要调整，则根据三种情况的讨论，我们发现无论哪一种情况，在调整之后一定还保留着红色结点。有同学可能会质疑，情况 1 如果 G 到了根结点，则需要被染黑，但要注意的是，此时的 X 还是红色的，因此不管什么情况都是会保留红色结点

红黑树的删除¶

我们首先回忆普通二叉树的删除操作，主要有以下三种情况

如果X是叶子结点，直接删除即可
如果X只有一个孩子，直接用孩子替换X即可
如果X有两个孩子，找到X的后继Y，将Y的值赋给X，然后删除Y，这个Y一般而言是左子树的最大结点，或者是右子树的最小结点

第三种情况可以通过一步交换变成第一第二种情况中的一种，因为左子树的最大节点不可能有右结点，右子树的最小结点不可能有左结点

叶子结点的删除¶

对于第一种情况,如果X没有子节点,亦即X是叶子结点,那么我们可以直接删除X,并让NiL结点接替这个位置,相当于什么都没有干

内部叶子结点¶

所以对于红黑树的删除,缩减到了两种大情况

Case 1:X是有两个NiL结点的内部结点
Case 2:X只有一个NiL结点的内部结点
- Case 2-1:child是红色
- Case 2-2:child是黑色

如果X只有一个带有键值的子节点,此时如果X是红色,那么万事大吉,直接删除,让它的子节点接替它的位置,如果X是黑色,接替上来的结点是红色,直接染黑即可,如果接替的是NiL结点(Case 1),或者接替上来的是黑色结点(Case 2-2),我们该怎么办

解决方法十分聪明,直接给黑色结点(包括NiL结点)再加上一重黑色,变成 双黑结点 .此时第五条性质没有被破坏,但是我们凭空多了一种颜色,这自然是不行的,所以我们的想法是,将这一重黑色传递给上层的一个红色结点,或者没找到,直接往上推到根节点,让根结点变成双黑,而根节点从双黑变成黑色是完全没有影响的,这样就解决了问题

我们可以把双黑传递的情况分为以下四类,用子树代表更一般的情况(可能发生在传递的过程中,X代表双黑结点)

红色呢,救一下啊

情况1: X有红色的兄弟

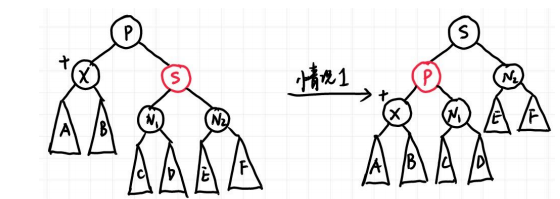
此时父结点一定是黑色,我们的想法很简单，兄弟是红色，那就希望兄弟能两肋插刀，把兄弟转上去，为了保持红黑树性质，很可惜只能把父亲染红，自己还承受双黑 debuff。但是好处在于，这个问题转化为了接下来的情况234中的一种,此时X的兄弟一定是黑色,因为这个兄弟之前是X红色兄弟的孩子:

情况2:X 的兄弟是黑色的，且兄弟的两个孩子都是黑色的

Note

根据距离划分为近、远侄子，用远近而不用左右是为了对称情况不混淆左右

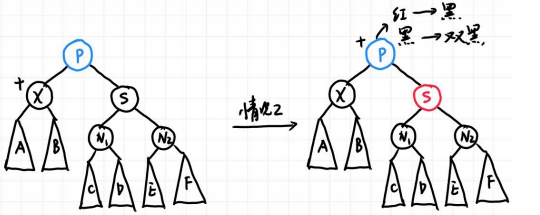
此时没有红色能救一下了,我们就把希望寄托于父节点,因为根节点一定能救,所以此时的做法就是将这一层的黑色往上推,将X的一层黑色去掉,将兄弟染红,父亲给一层黑色,如果父亲是红色,那么直接染黑即可,如果父亲是黑色,那么就又多了一层黑色

Key-point

如果情况2是情况1演变而来的,那么X的父节点一定是红色,此时问题可以直接解决

情况3:X 的兄弟是黑色的，且近侄子是红色,远侄子是黑色

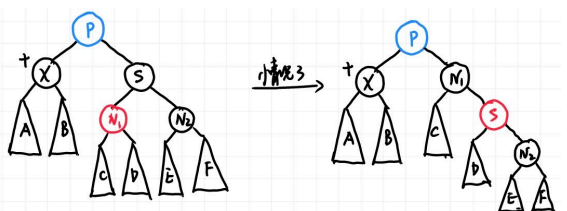
这时我们借用 AVL 树的想法，红色在父亲 P 的 RL 位置，因此做 single rotation 后会变成情况 4 的 RR 的情况

Note

也就意味着红色要给到 RR 的位置，这里有一个颜色的变化，用 RR 记忆很方便

情况4:X 的兄弟是黑色的，且远侄子是红色,近侄子是任意颜色

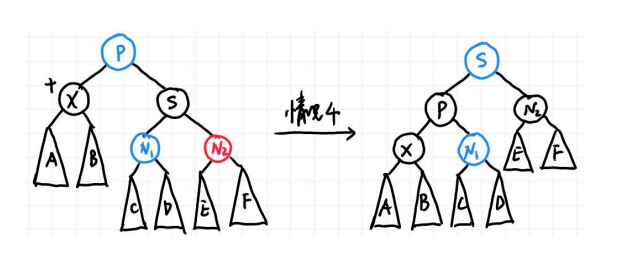
此时对应 AVL 树的 RR，于是再一次 single rotation 即可把双黑的一重黑丢给红色远侄子（即 X 和 N2 都变成黑色），但要注意为了保证红黑树性质的颜色变化，如果 P 一开始是黑色,那么旋转前后到N2的路径上黑色结点数目不变，都是2,如果P是红色,那么旋转前后到N2的路径上黑色结点数目增多，此时需要将S染红，P染黑,总的来说,可以交换P和S的颜色

吴一航学长的ADS讲义

首先我们最多用 $O(\log n)$ 的时间找到删除结点，最多 1 次交换和 1 个删除的操作。接下来如果删除后没有问题则到此结束；否则根据分析，情况 1、3和 4 在问题解决前最多进去一次，因为 4 可以直接解决，3 直接进入 4 然后解决，1 如果进入 3 和 4也可以马上解决，进入 2 后也因为父结点是红色可以马上解决。因此关键在于情况 2 可能出现很多次，但最多也只是树高 $O(\log n)$ 次，因为每次都会上推 1 格。总而言之，因为情况 1、3 和 4 在问题解决前最多进去一次，所以最多 3 次旋转加上 $O(\log n)$ 次颜色调整可以解决问题

Question

考虑将一个结点 X 插入红黑树 T0，得到红黑树 T1，然后紧接着下一步操作又立刻将 X 从 T1 删除得到 T2，请问 T0 和 T2 是否一定一样？若是，请给出清晰的证明；若不是，请举出反例。

B+树¶

Definition

A B+ tree of order ** $M$ ** is a tree with the following properties:

The root is either a leaf or has between $2$ and $M$ children.
All noneleaf nodes (except the root) have between $ \lceil \frac{M}{2} \rceil $ and $M$ children.
All leaves are at the same depth.

与红黑树的定义比起来，B+树的的定义就显得更为简单，我们只需要每个结点中储存的键值个数的限制和孩子个数的限制，以及所有键值都在叶节点中有存储。

Question

为什么根节点的孩子个数从2开始？

因为一开始插入到根结点爆炸时，根节点只能分裂成两个孩子

为什么非叶子结点的孩子个数要求是 $\lceil \frac{M}{2} \rceil$ ？

是因为插入到爆炸的时候就是分裂到这个数量

注意非叶子节点孩子个数的限制是 $\lceil \frac{M}{2} \rceil$，如果问的是key的个数，那么是 $\lceil \frac{M}{2} \rceil-1$

B+树搜索¶

根据 B+ 树定义，需要在非叶结点层逐层和存储的键值比较从而确定去哪一个孩子结点。因此时间复杂度有两个重要因素：一个是树的高度，另一个是每一层搜索需要的时间。树的高度非常好计算，最差的情况也是每个结点都存 $\lceil \frac{M}{2} \rceil$ 个结点，因此最大高度是 $O(\log_{⌈M/2⌉} N)$ 的。然后每一层因为键值是排好序的，因此用二分查找找到要去哪个孩子结点，复杂度为 $O(\log_2 M)$，综合可得搜索的时间复杂度为

\[ O(\log_2M \cdot \log_{⌈M/2⌉} N) = (\log_2 \frac{M}{2}+1) \cdot \frac{\log_2 N}{\log_2 \frac{M}{2}} = O(\log N) \]

B+树插入¶

伪代码如下

Btree  Insert ( ElementType X,  Btree T ) 
{ Search from root to leaf for X and find the proper leaf node;
Insert X;
while ( this node has M+1 keys ) 
{split it into 2 nodes with (M+1)/2 and (M+1)/2  keys,
 respectively;
 if (this node is the root)
 create a new root with two children;
check its parent;
}
}

Key-point

分裂时，以右半部分的最小孩子作为分裂后的索引，例如 2-3 树，根节点为（1,2,3）,插入4之后，分裂为（1,2）和（3,4）,根节点变为3，左孩子为（1,2）,右孩子为(3,4)

就是找到插入的位置，然后插入看结点是否放得下，放不下就分裂，如果分裂后子结点个数也过多则继续向上一层分裂，直到根结点孩子爆满则将根结点分裂并生成新的根结点，当然还要注意即使不分裂也可能需要按 B+ 树定义更新上层结点。我们知道树有 $O(\log_{⌈M/2⌉} N) $层，每层操作最多是 $O(M)$ 的（如更新结点或者分裂，无非就是更改 $O(M)$ 个键值以及修改 $O(M)$ 个父子指针），因此整体时间复杂度为

\[O(M \cdot \log_{⌈M/2⌉} N) = O(\frac{M}{\log M} \log N)\]

B+树删除¶

想法很简单，因为只需把插入时分裂结点改为合并键值或孩子数量少的结点，当然需要注意的是，为了确保合并后键值数量不会超过 M 且减少合并次数，可以先看看兄弟结点是不是键值还很多，多的话拿一个过来即可，事实上整体时间复杂度和插入分析类似，也为 $O(\frac{M}{\log M} \log N)$