Greedy Algorithm¶
约 3024 个字 56 行代码 预计阅读时间 11 分钟
贪心算法保证每次选择都是局部最优的,如果局部最优也是全局最优,那么贪心算法就是正确的。
活动选择问题¶
问题描述
给定一个活动集合 \(S = \{a_1, a_2, \ldots, a_n\}\),其中每个活动 \(a_i\) 都有一个开始时间 \(s_i\) 和结束时间 \(f_i\),且 \(0 \leqslant s_i < f_i < \infty\)。如果活动 \(a_i\) 和 \(a_j\) 满足 \(f_i \leqslant s_j\) 或 \(f_j \leqslant s_i\),则称活动 \(a_i\) 和 \(a_j\) 是兼容的(即二者时间不会重合)。活动选择问题就是要找到一个最大的兼容活动子集。
动态规划
我们假设输入中是按照 \(n\) 个活动结束时间从小到大排列的。可以设计出两种动态规划的递推式来解决这个问题:
- 设 \(S_{ij}\) 表示活动 \(a_i\) 和 \(a_j\) 之间的最大兼容活动集合(开始时间在 \(a_i\) 结束之后,结束时间在 \(a_j\) 开始之前),其大小记为 \(c_{ij}\),那么我们有
这一解法的思想更接近矩阵乘法顺序问题,我们会选择中间的最优解然后分为左右子问题递归。
- 设 \(S_i\) 表示活动 \(a_1, a_2, \ldots, a_i\) 的最大兼容活动集合,其大小记为 \(c_i\),那么我们有
其中 \(k(i)\) 表示在 \(1 \leqslant k \leqslant i\) 中,\(f_k \leqslant s_i\) 且\(c_k\)最大的\(k\),即不与\(a_i\)冲突的最晚结束的活动这一思想更接近背包问题的思路,即我们考虑最后一个是否在解中,分成两种情况考虑。
Property
两种动态规划的时间复杂度都是 \(O(n^3)\),可以优化为 \(O(n^2)\)。
贪心算法
很多时候使用贪心只需要一次遍历就能找到最优解,这里我们可以使用贪心算法来解决活动选择问题。
我们依次排好序后选择 不冲突的结束时间最早的事件(或者从后往前看依次选择不冲突的开始时间最晚的事件) 加到最优解中
Proof
假设 \(a_k\) 是 \(a_1, a_2, \ldots, a_n\) 中结束时间最早的活动,那么 \(a_k\) 一定是某个最大兼容活动子集的一部分。因为如果 \(a_k\) 不在最大兼容活动子集中,那么我们可以将 \(a_k\) 替换为最大兼容活动子集中的某个活动,这样我们就得到了一个更大的兼容活动子集,这与我们的假设矛盾。
Property
如果活动已经排好序排序,那么贪心算法的时间复杂度是 \(O(n)\)。
否则需要排序,时间复杂度是 \(O(n \log n)\)。
Extra
-
加权活动选择问题:每个活动 \(a_i\) 都有一个权重 \(w_i\),我们要找到一个最大权重的兼容活动子集。
此时动态规划仍然可行,但是贪心算法不可行;
-
区间调度问题:我们现在的问题不再是最大化兼容集合的大小或者权重,而是所有活动都必须举办,考虑将所有活动分配到最少的教室中,使得每个教室内的活动不冲突。
我们可以用贪心算法解决这个问题:将所有活动按照开始时间排序,设置初始教室数量为 1,然后从前往后遍历。每次选择一个活 动时,我们都看当前的教室中的活动有没有不冲突的,如果有就直接放进对应的教室,如果全部冲突则新开一个教室
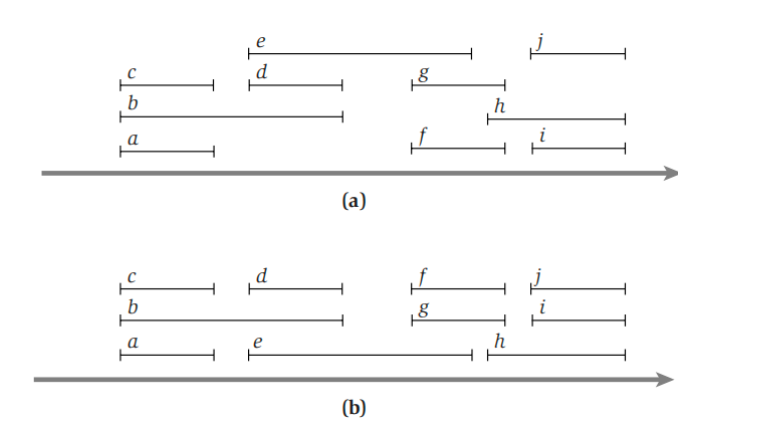
(a) 展示了一个例子,我们可以看到最多同一时间有三个活动那同时进行,所以我们需要三个教室,如果需要四个教室,说明至少某一时刻有四个活动同时进行,这是不可能的。
(b) 展示了一个贪心算法的实现,我们可以看到从前往后,我们首先选择a,b,c,发现三个活动同时进行,所以开出三个教室,然后到e,d,发现其可以放进不冲突的c,a教室中,以此类推,最后用三个教室解决问题
调度问题¶
问题描述
假设我们现在有 \(n\) 个任务,每个任务 \(i\) 都有一个正的完成需要的时间 \(li\) 和一个权重 \(wi\)。假定我们只能按一定顺序依次执行这些任务,不能并行。很显然的,我们有 \(n!\) 种调度方法,我们记 \(\sigma\) 为某一种调度,那么在调度 \(\sigma\) 中,任务 \(i\) 的完成时间 \(Ci(\sigma)\)是 \(\sigma\) 中在 \(i\) 之前的任务长度之和加上 \(i\) 本身的长度。换句话说,在一种调度中,一个任务的完成时间 就是这个任务从整个流程开始到它自己被执行完毕总共执行的时间。我们的目标是最小化加权完成时
我们运用贪心算法来解决这个问题,首先,如果它们权重一样,那么我们每次都选择时间最短的任务。如果时间一样,我们可以将任务按照权重排序,然后依次选择权重最大的。那么现在我们要同时考虑权重最大,时间最短的任务:
-
计算每个任务的\(w_i-l_i\),从大到小降序调度任务(\(l_i-w_i\),从小到大)
-
\(\dfrac{w_i}{l_i}\),从大到小降序调度任务(\(\dfrac{l_i}{w_i}\),从小到大)
Eg
有两个任务,\(l1 = 5, l2 = 2, w1 = 3, w2 = 1\)两种方法会返回不同的结果,而第二种才能返回最优解。
当然这只能说明第一种必然是错误的,对于第二种的正确性仍然需要证明。
Proof
调度问题的贪心选择性质 令 \(i\) 是当前 \(w_i / l_i\) 最大的任务,则在当前问题下,必一定存在将 \(i\) 排在首位的最优调度方式。
我们仍然使用“交换参数法”:假设有一个最优解 \(C\),如果它的第一个任务是 \(i\),结论成立。如果不是,我们考虑将 \(i\) 不断与前一个任务交换,直到换到第一个位置的过程。假设现在排在 \(i\) 前面的一个任务是 \(j\),我们知道一定有
又所有数都正,故有 \(w_i l_j - w_j l_i \geqslant 0\)。不难看出,\(i\) 和 \(j\) 交换前后其它的任务加权时间完全没有变化。变化仅在于 \(i\) 和 \(j\)。设在 \(i\) 前面的总时间为 \(t\),则交换前 \(i\) 和 \(j\) 的加权时间和为
交换后为
二者作差化简有
故由:往前换,加权时间和一定不会变大,故仍然保证最优解。那么我们就可以不断把 \(i\) 往前换,直到它在第一个位置,这样就证明了贪心选择性质。
调度问题的最优子结构 在调度问题 \(S\) 中,我们用贪心策略选出 \(w_i / l_i\) 最大的 \(i\) 对应的任务后,剩下的子问题 \(S_1\)(即在除去 \(i\) 的任务中寻找一个最小化加权完成时间之和的解)的最优解 \(C_1\) 和 \(i\) 一起一定构成了原问题的一个最优解 \(C\)。
和贪心选择问题完全一致,非常通过的结论就是用反证法想法:如果 \(C\) 不是最优解,那么必定有一个最优解 \(C'\),它对应的加权完成时间记为 \(T'< T\),其中 \(T\) 是 \(C\) 对应的加权完成时间之和。
根据贪心选择性质,如果把 \(C'\) 中的 \(i\) 不断通过相邻交换换到第一个位置,情况一定不会变差,因此得到解 \(C''\),我们将这一过程的最优记为 \(C''\)。于是 \(C''\) 在选择了 \(i\) 之后,剩下的选择实际也是\(S_1\)的一个解,,由于 \(T′ < T\),这表明 \(C''\) 中对应的 \(S1\) 的解必定比 \(C1\) 更好,但我们知道 \(C1\) 是最优解,因此得到矛盾。所以 \(C1\) 和 \(i\) 一起一定构成了原问题的一个最优解 \(C\)。综上以反证法,我们最终得以验证了问题的最优解可以通过贪心 + 最优子结构的方式得到。
Extra
-
最小化最大延时:设有 \(n\) 个任务,每个任务 \(j\) 具有一个完成需要的时间 \(t_j\),以及一个截止日期 \(d_j\)。我们只能依次完成这些任务,不能并行
三个任务长度分别为 1、2、3,截止日期分别为 2、4、6,按如图方式排序,所有任务都能在截止前完成。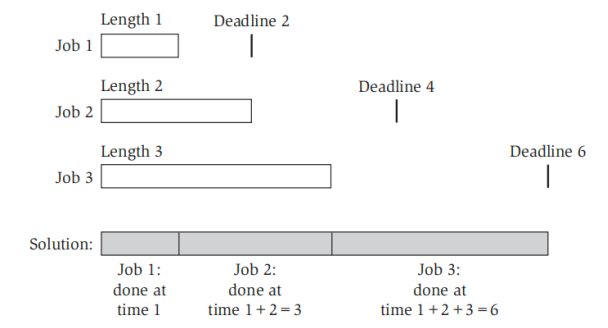
-
按照用时排序,用时短的先完成;这种做法是错误的,因为用时短的任务有可能截至日期很长
-
按照\(d_j-t_j\)从小到大排序,这似乎看起来正确,但是实际上也是错误的,例如任务1用时1天,3天后截至,任务二用时10天,11天后截至,这样排序后任务1会在截至日期前完成,但是任务2会在截至日期后完成;
-
-
实际上上面两种思路出现了矛盾,对于第一种,完成时间短的应该早完成,在第二种思路中,完成时间短的,冗余时间反而大,应该晚完成;这就陷入了一个尴尬的境地,我们不知道\(t_j\)应该被如何考虑----答案是我们不需要考虑,我们只需要考虑\(d_j\)即可,我们可以将任务按照截至日期排序,然后依次完成。
Huffman 编码¶
离散没学懂的,弥补一下
哈夫曼编码希望找到一个字母表的期望长度最小(依据字母出现频率)的前缀编码,在之前最优二叉搜索树的讨论中我们似乎有一个类似的目标,但那里我们是希望最小化搜索的期望时间,并没有前缀编码的需求。事实上,哈夫曼编码具有非常强的信息论背景。
信息熵与前缀编码¶
对于一个离散型随机变量\(X\),其信息熵定义为
Note
在平均意义下,信息熵可以理解为对于一个随机变量 \(X\),我们需要多少比特来表示它。
Eg
- 考虑一个服从均匀分布且有 32 种可能取值的随机变量 X。为了确定一个结果,需要一个能容纳 32 个不同值的标识,因此用 5 个比特足矣。而其信息熵为
- 有 8 匹马参加的一场赛马比赛,它们的获胜概率分别为
假定我们要把哪匹马会赢的信息告诉给别人,其中一个策略是发送胜出的马的编号,这样对于任何一匹马都需要 3 个比特。但由于概率不是均等的,明智的方法是对概率大的马用更短的编码,对概率小的马用更长的编码。例如使用以下编码:0, 10, 110, 1110, 111100, 111101, 111110, 111111,这样平均每匹马需要 2 个比特,比等长的比特数更短。
算法描述¶
我们以二叉树的形式来构建编码树,信息都存储在叶子节点上,非叶子节点不存储信息。从根节点到叶子节点的路径上的 0 和 1 分别代表左右子树。
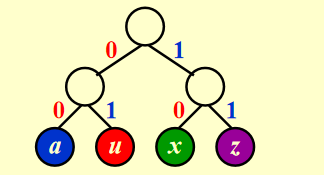
例如我们要编码一串\(aaaxuaxz\)像这样的一颗树,a的前缀编码是00,u是01,等等。
如果某个字符在深度为 \(d\) 的位置,那么它的编码长度为 \(d\),其出现的频率为 \(f\),那么它的总编码长度为 \(f \cdot d\)。我们的目标是最小化所有字符的总编码长度。
如果根据频率来编码,我们可以构建这样一颗树

构造哈夫曼编码树
具体来说,我们可以这样构造哈夫曼编码树
构造哈夫曼编码树的具体步骤:
- 统计频率:
给定一组待编码的字符,每个字符都有一个出现频率(或者权重)。首先,需要统计每个字符的频率。
- 创建优先队列(最小堆):
根据字符的频率,将所有字符作为节点,并将它们放入一个优先队列(最小堆)中。堆中的每个元素是一个节点,节点的值为字符的频率。优先队列保证每次能够快速取出频率最小的两个节点。
- 构建哈夫曼树:
从最小堆中反复取出两个最小频率的节点,创建一个新的父节点。这个父节点的频率是两个子节点频率之和。新的父节点不代表某个具体的字符,而是作为一个中间节点,连接两个原始节点(即两个字符的频率节点)。将新生成的父节点插回最小堆中。这个过程不断重复,直到堆中只剩下一个节点为止。最终剩下的节点就是哈夫曼树的根节点。
- 生成编码:
一旦哈夫曼树构建完成,就可以为每个字符分配编码。通过从树的根节点出发,沿着每一条路径到达叶子节点来确定编码。通常,沿左边的边分配"0",沿右边的边分配"1"。
- 叶子节点所对应的编码即为哈夫曼编码。
代码实现
import heapq
class Node:
def __init__(self, char, freq):
self.char = char # 字符
self.freq = freq # 频率
self.left = None # 左子树
self.right = None # 右子树
def __lt__(self, other):
return self.freq < other.freq
def build_huffman_tree(freqs):
# 创建优先队列(最小堆),每个元素是一个Node对象
heap = [Node(char, freq) for char, freq in freqs.items()]
heapq.heapify(heap)
while len(heap) > 1:
# 取出两个频率最小的节点
left = heapq.heappop(heap)
right = heapq.heappop(heap)
# 创建一个新的父节点
merged = Node(None, left.freq + right.freq)
merged.left = left
merged.right = right
# 将新的节点插回堆中
heapq.heappush(heap, merged)
# 返回最终的哈夫曼树的根节点
return heap[0]
def generate_huffman_codes(node, prefix="", codebook={}):
if node is not None:
if node.char is not None:
# 叶子节点,存储编码
codebook[node.char] = prefix
else:
# 递归遍历左右子树
generate_huffman_codes(node.left, prefix + "0", codebook)
generate_huffman_codes(node.right, prefix + "1", codebook)
return codebook
伪代码
void Huffman ( PriorityQueue heap[ ], int C )
{ consider the C characters as C single node binary trees,
and initialize them into a min heap;
for ( i = 1; i < C; i++ ) {
create a new node;
/* be greedy here */
delete root from min heap and attach it to left_child of node;
delete root from min heap and attach it to right_child of node;
weight of node = sum of weights of its children;
/* weight of a tree = sum of the frequencies of its leaves */
insert node into min heap;
}
}
Huffman编码正确性¶
贪心选择性质¶
\(C\) 为一个字母表,其中每个字符 \(c \in C\) 都有一个频率 \(c.freq\).令 \(x\) 和 \(y\) 是 \(C\) 中频率最低的两个字符。那么存在 \(C\) 的一个最优前缀码,\(x\) 和 \(y\) 的码字长度相同,且只有最后一个二进制位不同(即在编码二叉树中,它们是兄弟节点)。
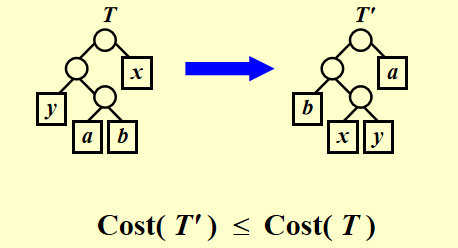
我们也可以用交换法,如上图,可以证明交换后的树所用的编码长度不会变大,如果原来的是最优解,那么交换后的也是最优解。
最优子结构¶
\(C\) 为一个字母表,其中每个字符 \(c \in C\) 都有一个频率 \(c.freq\)。令 \(x\) 和 \(y\)是 \(C\) 中频率最低的两个字符。令 \(C′\) 为 \(C\) 去掉字符 \(x\) 和 \(y\),加入一个新字符 \(z\) 后的字母表。我们给 \(C′\) 也定义频率集合,不同之处只是 \(z.freq = x.freq + y.freq\)。令 \(T′\) 为 \(C′\) 的任意一个最优前缀码树,那么我们可以将 \(T′\) 中叶结点 \(z\) 替换为一个以 \(x\) 和 \(y\) 为孩子的内部结点得到一个 \(C\) 的一个最优前缀码树 \(T\)。
Note
如果上面这一命题正确,那么我们每次合并 \(x\) 和 \(y\) 得到 \(z\) 之后,按照没有 \(x\) 和 \(y\),只有 \(z\) 的子问题继续推进我们的贪心算法可以得到 \(T′\) 这一子问题的最优解,它和合并 \(x\) 和 \(y\) 得到 \(z\) 这一前面已经验证正确性的贪心选择一起,就构成了整体的最优解。
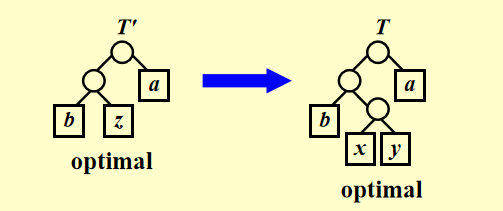
使用反证法证明
首先我们有
因为\(T'\)相当于把\(T\)中\(x,y\)上移一层,假设\(T\)不是最优解,那么存在一个更优解\(T''\),使得
即
则有
其中\(T'''\)是\(T''\)中\(x,y\)合并成\(z\)得到的树,这与\(T'\)是最优解矛盾,所以\(T\)是最优解,证毕。
