电动力学
法拉第电磁感应定律
\[
\Phi = \int_S \boldsymbol{B} \cdot d\boldsymbol{S}
\]
\[
\varepsilon = -\frac{d\Phi}{dt}
\]
Key-point
楞次定律已经蕴含在"-"号中,楞次定律是能量守恒定律在电磁感应中的体现
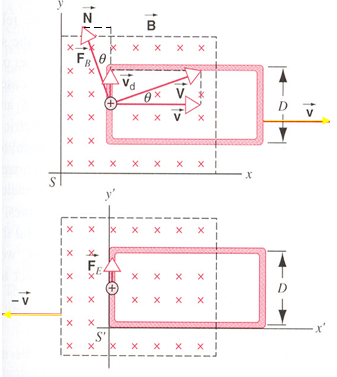
动生电动势
电荷受到的非静电力
\[
\boldsymbol{f} = q(\boldsymbol{v} \times \boldsymbol{B})
\]
实际上这个是洛伦兹力的分量
Proof
克服洛伦兹力的分量做功转化为非静电力做功,洛伦兹力总的不做功
\[
V=v+v_d \enspace F=N+f
\]
\[
F=qVB
\]
\[
dW_N=N (vdt)=F\sin\theta vdt=Fvdt\dfrac{v_d}{V}=F\dfrac{v}{V}(v_d dt)=F\cos\theta v_d dt=fv_d dt=dW_f
\]
动生电动势
\[
\varepsilon =\oint \boldsymbol{E} \cdot d\boldsymbol{l}=\oint \dfrac{\boldsymbol{f}}{q}d\boldsymbol{l}= \oint (\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{l}
\]
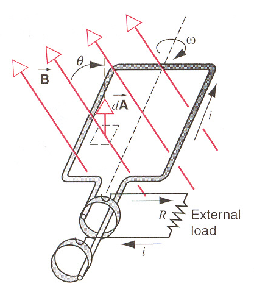
发电机
\[
\Phi = \boldsymbol{B} \cdot \boldsymbol{S} =BS\cos\theta=BA\cos\omega t
\]
\[
\varepsilon = -\dfrac{d\Phi}{dt} = BA\omega\sin\omega t
\]
感生电动势
涡旋电流
\[
\varepsilon = \oint \boldsymbol{E} \cdot d\boldsymbol{l}
\]
Proof
做功相等
\[
\varepsilon q_0=q_0 E_{induce} l
\]
\[
\varepsilon = E_{induce} l
\]
\[
\varepsilon = \oint \boldsymbol{E} \cdot d\boldsymbol{l}
\]
这提供了一种求出感生电场的方法
Example
磁场静止,动生电动势\(\varepsilon=BDv\)
磁场运动,感生电动势
\[
\varepsilon=\oint E dl=ED=BDv
\]
\[
E=v \times B
\]
变化的磁场
\[
\varepsilon = -\frac{d\Phi}{dt}=-A \frac{dB}{dt}
\]
推广电场环路定律
\[
\oint (\boldsymbol{E_{sta}+E_{ind}}) \cdot d\boldsymbol{l} =0+( -\frac{d\Phi}{dt})
\]
\[
\Phi = \iint \boldsymbol{B} \cdot d\boldsymbol{S}
\]
\[
\oint \boldsymbol{E} \cdot d\boldsymbol{l} = -\frac{d\Phi}{dt}= - \iint \frac{\partial \boldsymbol{B}}{\partial t} \cdot d\boldsymbol{S}
\]
运用stokes公式
\[
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
\]
Danger
在涡旋电场中,环路积分并不是0,所以在涡旋电场中不能使用电势的概念
电感
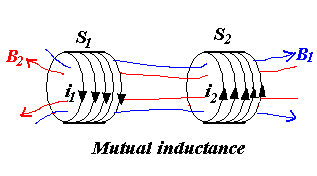
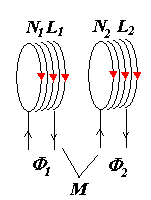
互感
\(i_1\)产生的磁场会使得\(s_2\)感应出\(\varepsilon_2\)
\(i_2\)产生的磁场会使得\(s_1\)感应出\(\varepsilon_1\)
由\(s_1\)在\(s_2\)上导致的磁通匝链数
\[
\Psi_{12} \propto N_2A_2B_1 \propto N_2\Phi_1 = M_{12}i_1
\]
由\(s_2\)在\(s_1\)上导致的磁通匝链数
\[
\Psi_{21} \propto N_1A_1B_2 \propto N_1\Phi_2 = M_{21}i_2
\]
\[
M_{12} = \frac{\Psi_{12}}{i_1} = \frac{N_2 \Phi_{12}}{i_1}; \quad \varepsilon_2 = -\frac{d\Psi_{12}}{dt} = -M_{12} \frac{di_1}{dt}, \quad (i_1 \text{ change})
\]
\[
M_{21} = \frac{\Psi_{21}}{i_2} = \frac{N_1 \Phi_{21}}{i_2}; \quad \varepsilon_1 = -\frac{d\Psi_{21}}{dt} = -M_{21} \frac{di_2}{dt}, \quad (i_2 \text{ change})
\]
互感系数
如上的\(M_{12}\)和\(M_{21}\)就是被称为互感系数,单位为亨利(Hery)
\[
1H=1\dfrac{Wb}{A}
\]
常见的有\(mH,\mu H\)等
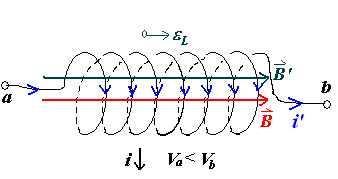
自感
类似的有
\[
\Psi = NBA =Li
\]
\[
\varepsilon_{L}= -\dfrac{d\Psi}{dt}=-L\dfrac{di}{dt} =V_b-V_a
\]
其中\(L\)被称为自感系数
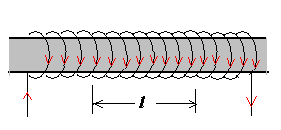
通电螺线管的自感系数
\(n\)为单位长度的匝数
磁场强度
\[
B = \mu_0 n i
\]
磁通匝链数
\[
\psi = N \Phi_B = n l BA = \mu_0 n^2 i l A
\]
自感系数
\[
L = \frac{\psi}{i} = \mu_0 n^2 l A = \mu_0 n^2 V
\]
单位体积的自感系数
\[
L_v = \frac{L}{V} = \mu_0 n^2
\]
单位长度的自感系数
\[
L_l = \frac{L}{l} = \mu_0 n^2 A
\]
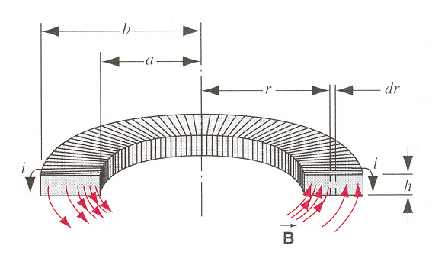
长方形截面螺绕环
\[
\int \mathbf{B} \cdot d\mathbf{l} = \mu_0 Ni
\]
\[
B = \frac{\mu_0 i N}{2 \pi r}
\]
\[
\Phi_B = \int \int \mathbf{B} \cdot d\mathbf{A} = \int_a^b \frac{\mu_0 i N}{2 \pi r} h dr
\]
\[
= \frac{\mu_0 i N h}{2 \pi} \int_a^b \frac{dr}{r} = \frac{\mu_0 i N h}{2 \pi} \ln \frac{b}{a}
\]
\[
\therefore L = \frac{N \Phi_B}{i} = \frac{\mu_0 N^2 h}{2 \pi} \ln \frac{b}{a}
\]
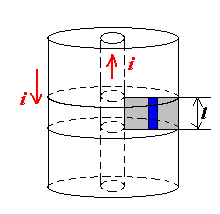
同轴电缆
\[
\int \mathbf{B} \cdot d\mathbf{l} = \mu_0 i,
\]
\[
B = \frac{\mu_0 i}{2 \pi r}
\]
\[
\Phi_B = \iint \mathbf{B} \cdot d\mathbf{A} = \int_{R_1}^{R_2} Bl \, dr
\]
\[
= \frac{\mu_0 il}{2 \pi} \int_{R_1}^{R_2} \frac{dr}{r} = \frac{\mu_0 il}{2 \pi} \ln\left(\frac{R_2}{R_1}\right)
\]
\[
\therefore L = \frac{\Phi_B}{i} = \frac{\mu_0l}{2 \pi} \ln\left(\frac{R_2}{R_1}\right)
\]
线圈拼接
其互感系数为
\[
M=\sqrt{L_1L_2}
\]
自感系数为
顺接
\[
L=L_1+L_2+2M
\]
反接
\[
L=L_1+L_2-2M
\]
材料的磁性质
在电容器中间插入电介质,可以让电容增大
\[
C=\kappa_e C_0
\]
在通电螺线管中插入铁磁材料,同样可以为自感系数增大
\[
L=\kappa_m L_0
\]
其中\(\kappa_m\)被称为磁导率
对于顺磁性材料,其磁导率约为1;对于铁磁性材料,其磁导率远大于1(\(10^3 \sim 10^4\))
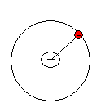
价电子的磁偶极矩
\[
\mu = iA
\]
\[
i = \frac{e}{T} = \frac{e}{2\pi r/v} = \frac{ev}{2\pi r}
\]
\[
\therefore \mu = iA = \frac{ev}{2\pi r} \cdot \left(\pi r^2\right) = \frac{1}{2} erv
\]
角动量为
\[
L = mvr
\]
所以
\[
\boldsymbol{\mu_l}=-\dfrac{e}{2m}\boldsymbol{L}
\]
\[
\boldsymbol{L}=\sqrt{L(L+1)}\dfrac{h}{2\pi}=\sqrt{L(L+1)}\hbar
\]
自旋的磁偶极矩
自旋角动量
| Particle |
Spin |
Type |
| Electron |
\( s = \frac{1}{2} \hbar \) |
Fermi |
| Proton |
\( s = \frac{1}{2} \hbar \) |
Fermi |
| Neutron |
\( s = \frac{1}{2} \hbar \) |
Fermi |
| Deuteron |
\( s = \hbar \) |
Bose |
| Alpha Particle |
\( s = 0 \) |
Bose |
Note
\(\hbar=\dfrac{h}{2\pi}\) 为约化普朗克常数
自旋磁矩
\[
\boldsymbol{\mu_s}=-\dfrac{e}{m}\boldsymbol{S}
\]
Key-point
总磁矩
\[
\boldsymbol{\mu}=\boldsymbol{\mu_l}+\boldsymbol{\mu_s}=-\dfrac{e}{2m}\boldsymbol{J}
\]
\[
\boldsymbol{J}=\boldsymbol{L}+2\boldsymbol{S}
\]
磁化强度\(M\)
在电容部分,我们引入了极化强度\(P\),在磁场部分,我们也类似的引入磁化强度\(M\)用于刻画磁性材料的磁性质
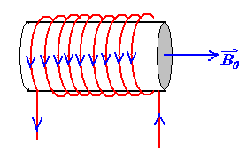
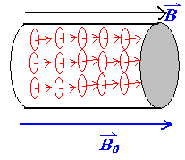
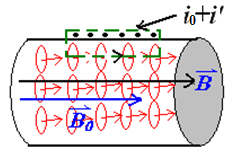
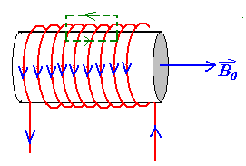
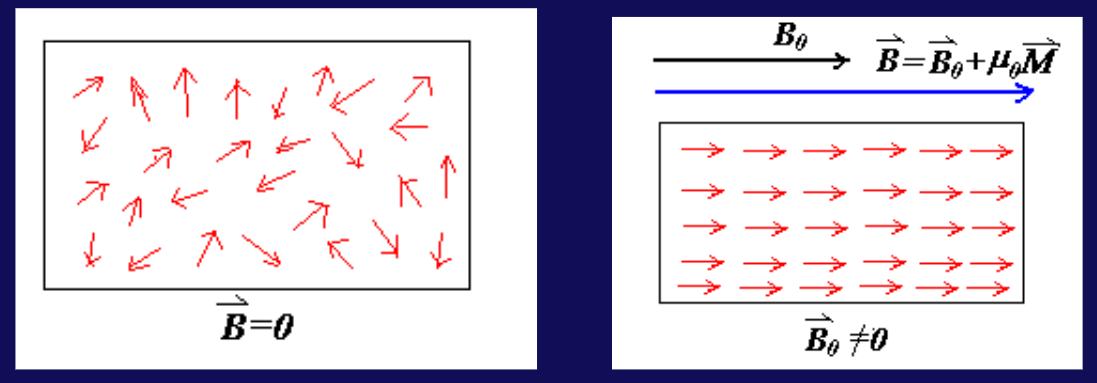
向通电螺线管中插入铁磁材料,原本杂乱无章的分子磁矩会受到磁场的作用,使得磁矩方向趋于一致,朝向磁场方向,在宏观上相当于在材料外围产生了一个电流
此时磁场被增强
\[
\boldsymbol{B}=\boldsymbol{B_0}+\boldsymbol{B'_{M}}
\]
磁化强度矢量
我们定义磁化强度矢量\(\boldsymbol{M}\)为单位体积内磁矩的矢量和,即
\[
\boldsymbol{M}=\dfrac{\sum \boldsymbol{\mu}}{V}
\]
我们也希望磁化强度矢量有类似于极化强度矢量的性质,即
\[
\oint \boldsymbol{M} \cdot d\boldsymbol{l} = \sum i_{in} \enspace (\oiint \boldsymbol{P} \cdot d\boldsymbol{A} = -\sum q_{in})
\]
\[
\boldsymbol{M} \cdot \boldsymbol{n} = j' \enspace (\boldsymbol{P} \cdot \boldsymbol{n} = \sigma_{surf})
\]
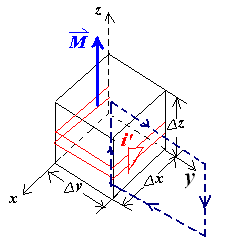
红色的是电流,电流面密度为
\[
j' = \frac{i}{\Delta z}
\]
只用除以\(\Delta z\)是因为我们只考虑到了表面的电流,即其向\(y\)的方向是没有的
\[
\Delta m = i' \cdot \Delta A = j' \Delta x \Delta y \Delta z
\]
\[
M = \frac{\Delta m}{\Delta V} = j'
\]
\[
M \cdot \Delta z = i'
\]
磁场强度
由环路定律
\[
\oint_L \boldsymbol{B} \cdot d\boldsymbol{l} = \mu_0 \sum_{inL} (i_0 + i') = \mu_0 \sum_{inL} i_0 + \mu_0 \oint_L \boldsymbol{M} \cdot d\boldsymbol{l}
\]
\[
\oint_L \left( \frac{\boldsymbol{B}}{\mu_0} - \boldsymbol{M} \right) \cdot d\boldsymbol{l} = \sum_{inL} i_0
\]
定义磁场强度为
\[
\boldsymbol{H} = \frac{\boldsymbol{B}}{\mu_0} - \boldsymbol{M}
\]
Note
磁化强度和磁场强度的关系为
\[
\boldsymbol{M}= \chi_m \boldsymbol{H}
\]
那么
\[
\boldsymbol{B}=\mu_0(\boldsymbol{H}+\boldsymbol{M})=\mu_0(1+\chi_m)\boldsymbol{H}= \mu_0 \kappa_m \boldsymbol{H}
\]
则 \(\kappa_m=1+\chi_m\)
Example
在上面的例子中,我们可以得到
\[
\oint_L \boldsymbol{H} \cdot d\boldsymbol{l} = \sum_{inL} i_0
\]
\[
\boldsymbol{H} \cdot \Delta \boldsymbol{l} = N i_0 \ \Rightarrow \ H = n i_0
\]
\[
B = \mu_0 \kappa_m H = \mu_0 \kappa_m n i_0 = \kappa_m B_0
\]
Idea
以这样的角度来看,磁场强度\(H\)和电场强度\(E\),磁感应强度\(B\)和电感应强度\(D\)的关系又是可以对应的
\[
D = \varepsilon_0 E+P=\varepsilon_0 \kappa_e E
\]
\[
B = \mu_0(H+M)=\mu_0 \kappa_m H
\]
磁化率与磁导率
|
顺磁 |
抗磁 |
铁磁 |
| \(\chi_m\) |
大于0但是小(\(10^{-6}\)) |
小于0但绝对值远小于1 |
与磁场强度有关 |
| \(\kappa_m\) |
大于1但是接近1 |
小于1但是接近1 |
与磁场强度有关(\(10^2 \sim 10^3\)) |
微观解释
顺磁材料(paramegnetic material)
原本杂乱无章的磁矩,在外磁场下,材料内部的磁矩会朝向磁场方向,但是与温度有关
居里定律
\[
\boldsymbol{M}=\chi_m\boldsymbol{H} \enspace \chi_m = \dfrac{C}{T}
\]
其中\(C\)为居里常数,\(T\)为温度
顺磁性的磁化率很小,磁化强度也很小,对磁场的影响很小
抗磁材料(diamagnetic material)
抗磁材料在没有外磁场的情况下,内部总磁矩为0;即:
\[
\boldsymbol{\mu}=\boldsymbol{0} \enspace \boldsymbol{J}=\boldsymbol{0}
\]
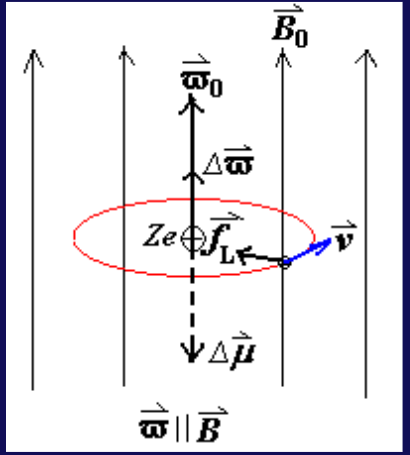
原本电子磁矩相消,加上外磁场后,电受到洛伦兹力,不管它是被加速还是被减速,都会产生一个与外磁场方向相反的磁矩(抗磁);
\[
\frac{Ze^2}{4\pi \varepsilon_0 r^2} = m \omega_0^2 r
\]
\[
\omega_0 = \left( \frac{Ze^2}{4\pi \varepsilon_0 m r^3} \right)^{1/2}
\]
\[
\frac{Ze^2}{4\pi \varepsilon_0 r^2} + e \omega r B = m \omega^2 r
\]
\[
\omega = \omega_0 + \Delta \omega
\]
\[
\Delta \omega = \frac{eB}{2m}
\]
增加的力与库仑力相比要小的多,产生的磁场也比顺磁材料感应的磁场小得多,对轨道半径几乎没有影响
其磁矩的变化为
\[
u = iA = \frac{ev}{2\pi r} \left( \pi r^2 \right) = \frac{1}{2} evr = \frac{e r^2}{2} \omega, \quad \boldsymbol{\mu_0} = -\frac{e r^2}{2} \boldsymbol{\omega_0}
\]
\[
\Delta \boldsymbol{\mu} = -\frac{e r^2}{2} \Delta \boldsymbol{\omega} = -\frac{e^2 r^2}{4m} \boldsymbol{B}
\]
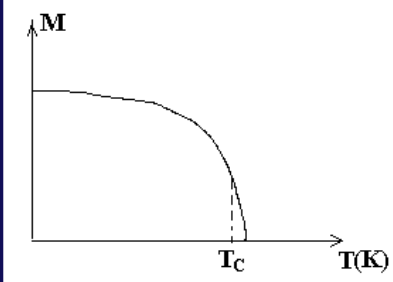
铁磁材料(ferromagnetic material)
初始的\(\mu \neq 0\),且近邻原子磁矩间存在强相互作用
磁化强度矢量与温度的关系
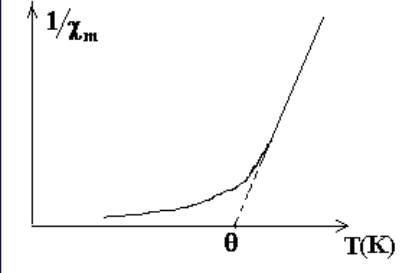
居里-维斯定理
\[
\chi_m=\dfrac{C}{T-\theta}
\]
磁畴
即使在没有外加磁场B的情况下,磁性材料中的磁偶极子(磁性小区域)也会倾向于在小范围内强烈地排列成特定的方向,形成所谓的“磁畴”。当施加外部磁场时,这些磁畴会重新排列,使得它们的方向一致,从而产生大的净磁化强度。
-
软铁磁体:指的是容易被磁化和退磁的磁性材料。它们在外部磁场作用下磁畴会有序排列,但磁场移除后磁畴会很快随机化。
-
硬铁磁体:指的是不易被退磁的磁性材料,例如某些特殊合金。它们在外部磁场移除后仍能保持磁畴的有序排列,因此具有较强的磁性。
-
永久磁体:通常指永久保持磁性的材料,例如稀土磁铁。它们的磁畴在没有外力作用下不会随机化,但可以通过施加外力(如磁场或震动)来改变磁畴的方向。
-
居里点:是磁性材料的一个物理特性,指的是材料由铁磁性变为顺磁性的转变温度。对于铁来说,这个温度是770摄氏度。
RL-回路
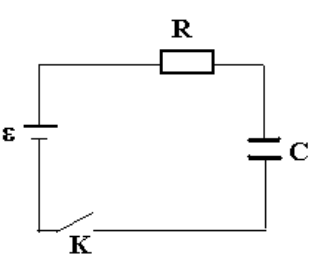
RC回路
\[
iR + \frac{q}{C} = \epsilon
\]
\[
\frac{dq}{dt} + \frac{1}{RC} q = \frac{\epsilon}{R}
\]
\[
q = C\epsilon\left(1 - e^{-t/RC}\right)
\]
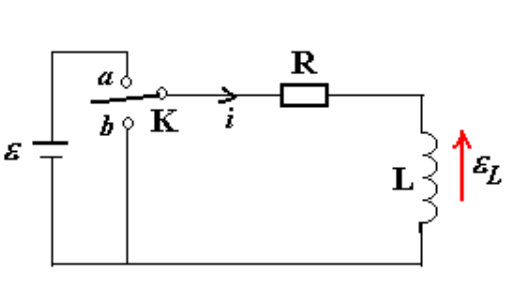
开关打到a
\[
iR + L \frac{di}{dt} = \varepsilon
\]
\[
\frac{di}{dt} = \frac{1}{L} \left( \varepsilon - iR \right) = -\frac{R}{L} \left( i - \frac{\varepsilon}{R} \right)
\]
\[
i - \frac{\varepsilon}{R} = C'e^{-\frac{R}{L}t}
\]
When \( t = 0, i = 0 \), thus \( C' = -\frac{\varepsilon}{R} \).
所以
\[
i = \frac{\varepsilon}{R}\left(1 - e^{-\frac{R}{L}t}\right) = \frac{\varepsilon}{R}\left(1 - e^{-\frac{t}{\tau_L}}\right)
\]
\[
\tau_L = \frac{L}{R}
\]
\[
V_L = -L \frac{di}{dt} = -\varepsilon e^{-\frac{t}{\tau_L}}
\]
时间常数\(\frac{R}{L}\)
对于电流
\[
i = \dfrac{\varepsilon}{R}(1-e^{-\frac{-Rt}{L}})
\]
最大是\(\dfrac{\varepsilon}{R}\),在\(t=L/R\)达到最大值的\(63\%\)
对于电压
\[
V_L = L\dfrac{di}{dt}=-\varepsilon e^{-\frac{-Rt}{L}}
\]
最大是\(\varepsilon\),在\(t=L/R\)达到最大值的\(37\%\)
开关打到b
\[
iR + L \frac{di}{dt} = 0
\]
\[
\frac{di}{dt} = -\frac{R}{L}i
\]
\[
i = i_0 e^{-\frac{R}{L}t}
\]
\(t=0\),\(i_0=\dfrac{\varepsilon}{R}\)
\[
i = \dfrac{\varepsilon}{R}e^{-\frac{R}{L}t}
\]
对于电流,在\(L/R\)时间后,电流减少到原来的\(37\%\)
对于电压,在\(L/R\)时间后,电压减少到原来的\(37\%\)
线圈的能量
Note
回忆电容器的能量
\[
U = \frac{1}{2} CV^2 \enspace u_e=\dfrac{1}{2}\varepsilon E^2
\]
\[
dW = -\varepsilon dq = -\varepsilon i dt = Lidi
\]
\[
W = \int_0^I Lidi = \frac{1}{2} LI^2
\]
Info
如果是互感线圈,那么 \(W=MI_1I_2\)
Key-point
磁场的能量密度
[
u_m = \dfrac{1}{2\mu_0}B^2
]
总结
\(\mu_B=\dfrac{1}{2}\boldsymbol{B} \cdot \boldsymbol{H}\)
\(\mu_E=\dfrac{1}{2}\boldsymbol{D} \cdot \boldsymbol{E}\)
电磁振荡
电容电场能和线圈磁场能量相互转化
Info
可以类比于弹簧振子,弹簧的势能和动能相互转化
\(q\)->弹簧的位移\(x\),\(i\)->弹簧的速度\(v\),\(\dfrac{1}{C}\)->弹簧的劲度系数\(k\),\(L\)->弹簧的质量\(m\)
\[
\omega=\dfrac{1}{\sqrt{LC}}
\]
Proof
\[
U = U_B + U_E = \frac{1}{2} Li^2 + \frac{1}{2} \frac{q^2}{C}
\]
\[
\frac{dU}{dt} = Li \frac{di}{dt} + \frac{q}{C} \frac{dq}{dt} = Li \frac{d^2 q}{dt^2} + \frac{q}{C} i = 0
\]
\[
\frac{d^2 q}{dt^2} + \frac{1}{LC} q = 0
\]
\[
\left( \frac{d^2 x}{dt^2} + \frac{k}{m} x = 0 \right)
\]
\[
\omega = \sqrt{\frac{k}{m}} = \frac{1}{\sqrt{LC}}
\]
阻尼和受迫振动
RLC电路
对于开关打到a和b的情况,我们可以得到
\[
L \frac{di}{dt} + iR + \frac{q}{C} =
\begin{cases}
\varepsilon & \text{K} \to a \\
0 & \text{K} \to b
\end{cases}
\]
即
\[
i = \frac{dq}{dt}, \quad
L \frac{d^2 q}{dt^2} + R \frac{dq}{dt} + \frac{1}{C} q =
\begin{cases}
\varepsilon & \\
0 &
\end{cases}
\]
过阻尼
当
\[
R^2 > \frac{4L}{C}
\]
此时为过阻尼震荡
 charging
charging
 discharging
discharging
临界阻尼
当
\[
R^2 = \frac{4L}{C}
\]
此时为临界阻尼震荡
\[
q = (A+Bt)e^{-\frac{R}{2L}t}+C\varepsilon
\]
图像与过阻尼相似,但是震荡得更快
欠阻尼
当
\[
R^2 < \frac{4L}{C}
\]
此时为欠阻尼震荡
做振幅不断减小的振动
 light damping
light damping
受迫振动和共振
如果外加电压为交流电,当变化频率与电路固有频率相同时,电路会发生共振
 共振
共振
Info
普通的天线无法同时接受很多的信号,如果很多人一起打电话,那么电线就会瘫痪掉,但是如果使用的是超导体天线,电阻很小,其振幅的宽度很小很小,不用担心共振的问题
最后,附上本人普通物理学(I)有关阻尼震荡的笔记,有空再敲上来吧