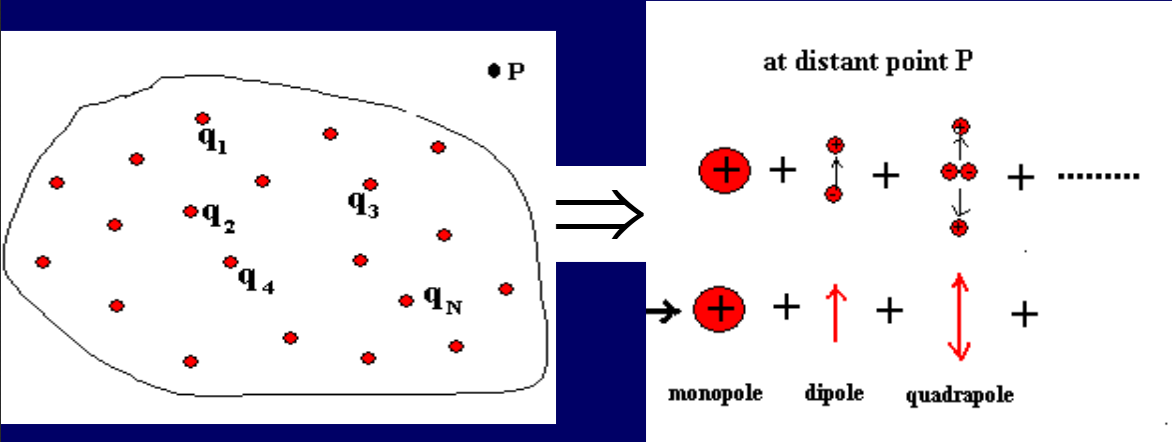
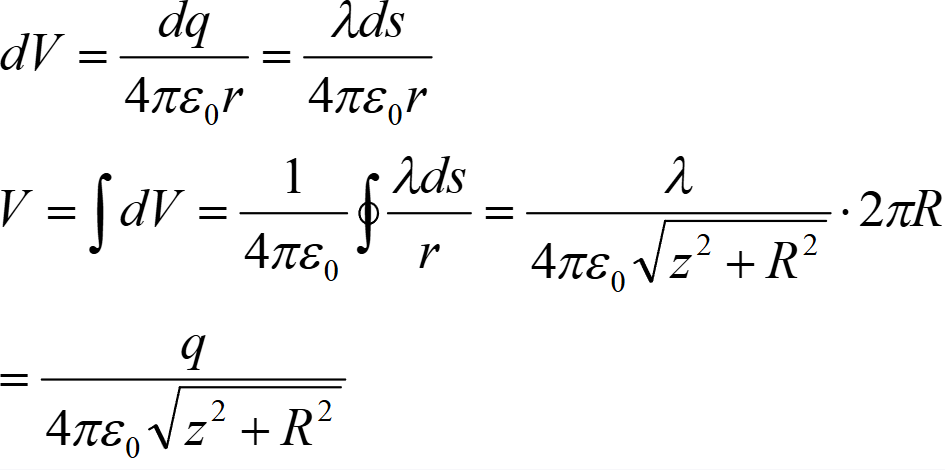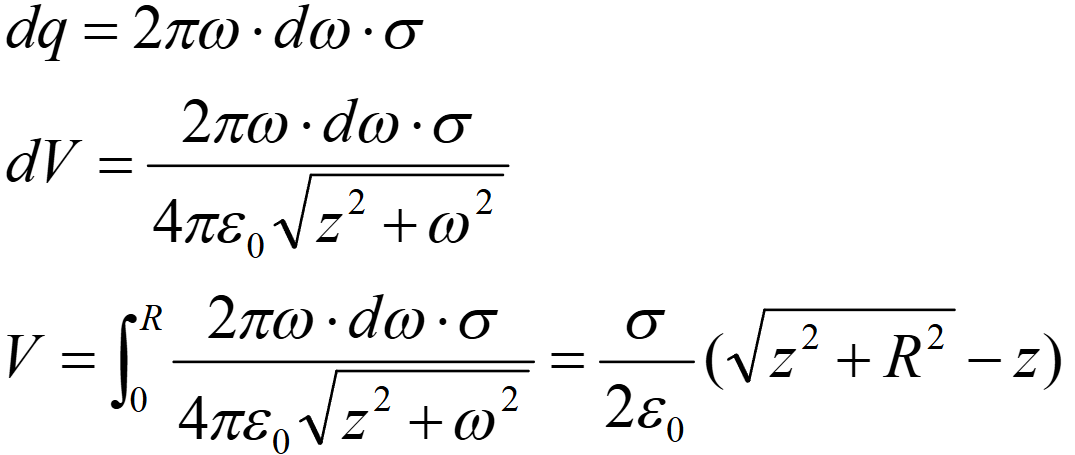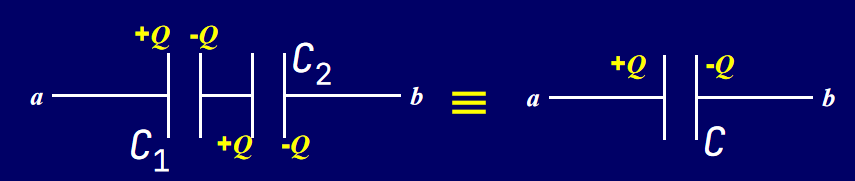电学部分
Electric Charge and Coulomb's Law(电荷和库仑定律)
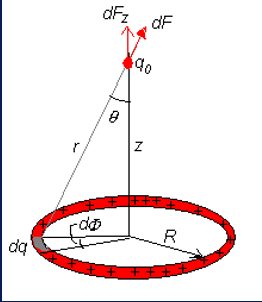
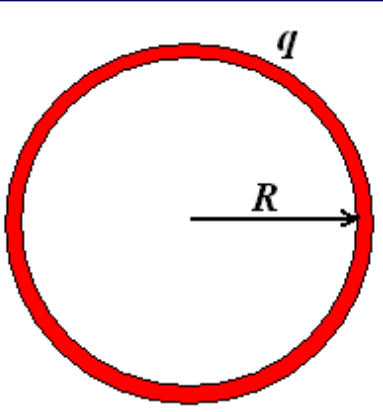
A ring of charge
Table of contents
对于一个均匀带电的圆环,距离其中心 \(z\) 的带电量为 \(q_0\) 所受的沿 \(Z\) 方向的力 \(F_z\)
先计算电荷密度
\[
\lambda = \frac{q}{2 \pi R}
\]
\[
dF = \frac{1}{4 \pi \epsilon_0} \frac{q_0 dq}{r^2} = \frac{1}{4 \pi \epsilon_0} \frac{q_0 \lambda Rd\phi}{(z^2 + R^2)}
\]
\[
F_z = \int dF_z = \int dF \cos \theta = \int \frac{q_0 \lambda Rd\phi}{4 \pi \epsilon_0 (z^2 + R^2)} \frac{z}{\sqrt{z^2 + R^2}}
\]
\[
= \frac{1}{4 \pi \epsilon_0} \int_0^{2\pi} \frac{q_0 \lambda Rz}{(z^2 + R^2)^{3/2}} d\phi
\]
\[
= \frac{1}{4 \pi \epsilon_0} \cdot \frac{q_0 q z}{(z^2 + R^2)^{3/2}} \bigg|_0^{2\pi}
\]
\[
= \frac{1}{4 \pi \epsilon_0} \cdot \frac{q_0 q z}{(z^2 + R^2)^{3/2}}
\]
Note
当 \(z\) 非常大,原式子就退化成了两个点电荷之间的相互作用
\[
z \to +\infty, F_z \to \frac{1}{4 \pi \epsilon_0} \dfrac{q_0q}{z^2}
\]
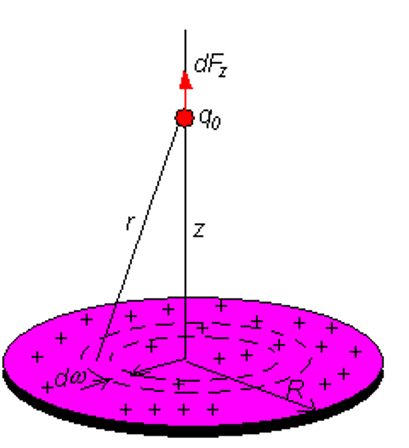
A disk of charge
如果是一个圆盘,\(F_z\) 可以用圆环来逼近
\[
\sigma = \frac{q}{\pi R^2}
\]
\[
dq = \sigma dA = \sigma(2 \pi \omega d\omega) = 2 \pi \sigma \omega d\omega
\]
\[
dF_z = \frac{1}{4 \pi \epsilon_0} \frac{q_0 (2 \pi \sigma \omega d\omega) z}{(z^2 + \omega^2)^{3/2}}
\]
\[
F_z = \frac{1}{4 \pi \epsilon_0} q_0 2 \pi \sigma z \int_0^{R} \frac{\omega d\omega}{(z^2 + \omega^2)^{3/2}}
\]
\[
= \frac{1}{4 \pi \epsilon_0} \cdot \frac{2 q_0 q}{R^2} \left( 1 - \frac{z}{\sqrt{z^2 + R^2}} \right)
\]
当 \(z\) 非常大,原式子就退化成了两个点电荷之间的相互作用(用Taylor展开分析)
\[ z \to +\infty, F_z \to \frac{1}{4 \pi \epsilon_0} \dfrac{q_0q}{z^2} \]
\[
\left( 1 - \frac{z}{\sqrt{z^2 + R^2}} \right) \to \left( 1- (1+\frac{R^{2}}{z^{2}})^{-\frac{1}{2}} \right) = \frac{R^{2}}{2z^{2}}
\]
Key-point
如果是一个无穷大的圆盘,那么\(R \to \infty\),此时
\(F_z = \dfrac{1}{4 \pi \epsilon_0} \dfrac{2q_0q}{R^2}\)
其电场为
\[
E_z = \frac{\sigma}{2 \varepsilon_0}
\]
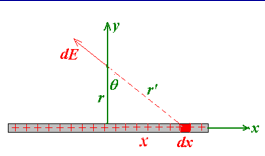
A infinite stick of charge
由于对称性,在\(x\)方向上没有电场
\[
\begin{align*}
dq &= \lambda dx = \lambda d(r \tan \theta) = \lambda r \sec^2 \theta d\theta \\
dE_y &= dE \cos \theta= \frac{1}{4 \pi \varepsilon_0} \frac{dq}{r'^2} \cos \theta \\
&= \frac{1}{4 \pi \varepsilon_0} \frac{\lambda r\cos^2 \theta \sec^2 \theta d\theta}{r^2} \cos \theta \\
&= \frac{1}{4 \pi \varepsilon_0} \frac{\lambda \cos \theta d\theta}{r}\\
E_y &= \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} dE_y = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{4 \pi \varepsilon_0} \frac{\lambda \cos \theta d\theta}{r} \\
&= \dfrac{\lambda}{2 \pi \varepsilon_0 r} \
\end{align*}
\]
Dipole(电偶极矩)
Definition
电偶极矩是描述带电粒子系统中电荷分布的物理量,通常用于量化两个相反电荷之间的分离程度和方向。在经典电磁学中,电偶极矩通常表示为一个矢量,其大小等于电荷量乘以电荷间的距离。
定义为:
\[
\boldsymbol{p} = q \cdot \boldsymbol{d}
\]
其中:
- \( q \) 是两个相反电荷的电荷量,
- \( \mathbf{d} \) 是从负电荷指向正电荷的矢量,表示两个电荷之间的距离。
电偶极矩的方向从负电荷指向正电荷,因此在分子或原子系统中,它反映了电荷不对称分布的程度。对于分子,电偶极矩的大小和方向对分子的化学性质和反应性有重要影响。
电偶极矩的单位通常是德拜(Debye,符号为 D),1 德拜大约等于 \( 3.33564 \times 10^{-30} \) 库仑·米。
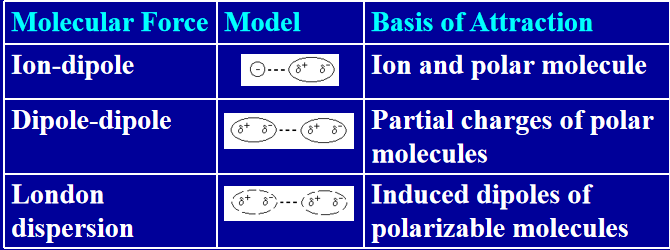
根据电偶极矩可以将分子间作用力分为几种类型
- 离子-偶极相互作用(Ion-Dipole Interaction)
离子-偶极相互作用发生在带电的离子和极性分子之间。当离子(如 \( \text{Na}^+ \) 或 \( \text{Cl}^- \))靠近一个有电偶极矩的分子(如水分子,H\(_2\)O)时,离子会与极性分子的部分正电荷或负电荷产生吸引力。
Eg
在盐溶解于水的过程中,水分子的极性部分(氧的负电部分或氢的正电部分)与钠离子或氯离子之间产生的吸引力是离子-偶极相互作用。这种相互作用有助于溶解过程。
- 偶极-偶极相互作用(Dipole-Dipole Interaction)
偶极-偶极相互作用发生在两个极性分子之间,这些分子都有永久的偶极矩。当一个分子的正电部分接近另一个分子的负电部分时,它们之间会产生吸引力。
Eg
像氯化氢 (HCl) 这样的极性分子之间的相互作用就属于偶极-偶极相互作用。HCl 分子的氯原子带负电,而氢原子带正电,这两种相反的电荷相互吸引,从而形成偶极-偶极相互作用。
- 伦敦色散力(London Dispersion Force)
伦敦色散力,又称为**瞬时偶极-诱导偶极力**,是一种在所有原子和分子之间都存在的弱相互作用力,特别是对于非极性分子。它是由瞬时的电子运动引起的,即在某个瞬间,分子或原子周围的电子云分布不均匀,形成瞬时偶极,这个瞬时偶极会诱导临近分子或原子产生相似的瞬时偶极,从而产生吸引力。
Eg
即使是像氮气 (N\(_2\)) 和氧气 (O\(_2\)) 这样的非极性分子,也存在伦敦色散力。这种相互作用虽然很弱,但对大多数非极性物质的凝聚力和熔沸点有重要影响。
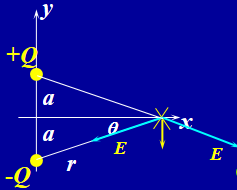
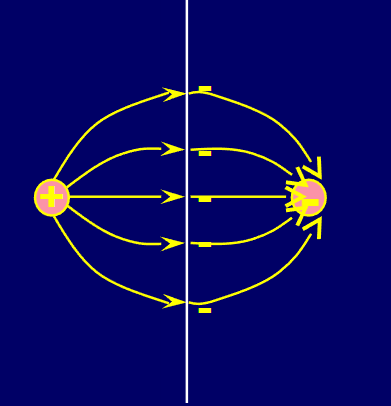
电偶极矩产生的电场
\[
E_x(x,0)=0(symmetry)
\]
\[
E_y(x,0) = -2 \cdot \frac{1}{4 \pi \varepsilon_0} \cdot \frac{Q}{r^2} \sin \theta
\]
\[
\sin \theta = \frac{a}{r}, \quad r^2 = x^2 + a^2
\]
\[
E_y(x,0) = -2 \cdot \frac{1}{4 \pi \varepsilon_0} \cdot \frac{Qa}{(x^2 + a^2)^{3/2}}
\]
Note
\[
for \ r>>a \\
E_y(r,0) = -2 \cdot \frac{1}{4 \pi \varepsilon_0} \cdot \frac{Qa}{r^3}
\]
如果考虑 \((0,y)\) 上的电场,则其在 \(x\) 方向上没有分量
\[
E_x(0,y)=0
\]
\[
\begin{align*}
E_y(0,y) &= \frac{Q}{4 \pi \varepsilon_0} \cdot \left(\frac{1}{(y-a)^2}-\frac{1}{(y+a)^2}\right)\\
&= \frac{Q}{4 \pi \varepsilon_0} \cdot \dfrac{4ay}{y^4(1-\frac{a^2}{y^2})^2}
\end{align*}
\]
Note
\[
for \ r>>a \\
E_y(0,r) = 4 \cdot \frac{1}{4 \pi \varepsilon_0} \cdot \frac{Qa}{r^3}
\]
Eg
北高峰上的天线和紫金港的分子
\(E\) 和 \(r^3\) 成反比
Key-point
电偶极矩的电场与距离\(r^3\)成反比,而点电荷的电场与距离\(r^2\)成反比,无穷长导线的电场与距离\(r\)成反比
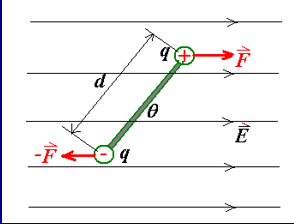
电偶极矩在电场中
\[
\tau = F \cdot \frac{d}{2} \sin \theta + F \cdot \frac{d}{2} \sin \theta = Fd \sin \theta = qEd \sin \theta
= pE \sin \theta
\]
\[
\boldsymbol{p}=q\boldsymbol{d} \\
\boldsymbol{\tau}= \boldsymbol{p} \times \boldsymbol{E}
\]
Key-point
电偶极矩在电场中受到的力矩会驱使电偶极矩旋转上与电场方向对齐
对于电偶极矩在电场中的势能
\[
\begin{align*}
W &=\int dw = \int_{\theta_0}^{\theta} \tau \cdot d\theta = - \int_{\theta_0}^{\theta} pE \sin \theta d\theta \\
&= pE(\cos \theta - \cos \theta_0) \\
\Delta U &= U(\theta) - U(\theta_0)=-W\\
&= pE(\cos \theta_0 - \cos \theta)\\
\theta_0 &= \frac{\pi}{2}, U(\theta_0) = 0\\
U(\theta) &= -pE\cos \theta= -\boldsymbol{p} \cdot \boldsymbol{E}
\end{align*}
\]
第一个式子的负号是因为力矩与角度的变化方向相反
Gauss's Law(高斯定理)
电场的高斯定理
Definition
The net electric flux through any closed surface is proportional to the charge enclosed by that surface.
\[
\Phi = \oiint \boldsymbol{E} \cdot d\boldsymbol{A} = \frac{q_{enc}}{\varepsilon_0}
\]
E不一定只由q产生,但是q只用计算被包裹住的电荷
在数学分析二中,我们也知道Gauss公式,即:
Note
设 \(\Omega\) 是分段光滑的封闭曲面构成的二维单连通区域,函数 \(P(x,y,z),Q(x,y,z),R(x,y,z)\) 在 $\Omega $ 上具有连续偏导数,
则
\[
\iiint_{\Omega} \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right) dV = \iint_{\partial \Omega} Pdydz + Qdzdx + Rdxdy
\]
将两者结合起来,我们就可以得到高斯定理的微分形式
\[
\Phi=\oiint \boldsymbol{E} \cdot d\boldsymbol{A} = \iiint \nabla \cdot \boldsymbol{E} dV
\]
而
\[
\frac{q_{enc}}{\varepsilon_0}= \iiint \frac{\rho}{\varepsilon_0} dV
\]
所以
\[
\nabla \cdot \boldsymbol{E} = \frac{\rho}{\varepsilon_0}
\]
Key-point
运用高斯定理可以通过电荷求电场,也可以通过电场求电荷,关键在于高斯面的选取,一般而言,选取球面,圆柱面,或者长方体表面更加方便计算,高斯定理只是再计算一些具有特殊对称性物体时,非常的方便,对于一般的物体,还是要用库仑定律来计算
Note
我们知道导体内部的电场是0,由高斯定理,导体的内部没有电荷,所以其电荷分布在表面。
静电场的环路定律
The circuit Law of the electrostatic field
\[
\oint \boldsymbol{E} \cdot d\boldsymbol{l} = 0
\]
then
\[
\nabla \times \boldsymbol{E} = 0
\]
这个是由Stokes定理推出的,即:
Note
设 \(\Omega\) 是光滑的曲面,其边界 \(\partial \Omega\) 是分段光滑的闭曲线函数 \(P(x,y,z),Q(x,y,z),R(x,y,z)\) 在 $\Omega,\partial \Omega $ 上具有连续偏导数,
则
\[\begin{align*}
\oint_{\partial \Omega} Pdx + Qdy + Rdz &= \iint_{\Omega} \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) dydz + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) dzdx + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dxdy\\
&= \left\lvert \begin{matrix} \cos \alpha & \cos \beta & \cos \gamma \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{matrix} \right\rvert dS\\
&= \left\lvert \begin{matrix} dydz & dzdx & dxdy \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{matrix} \right \lvert\\
&= \iint_{\Omega} \nabla \times \boldsymbol{F} \cdot d\boldsymbol{S}
\end{align*}\]
Electric Potential(电势)
电势能与电势
电势是电场中某一点的物理量,定义为单位正电荷在该点所具有的电势能。具体来说,电势 \( V \) 可以表示为:
\[ V = \frac{U}{q} \]
其中 \( U \) 是电势能,\( q \) 是电荷量。电势是一个标量,通常相对于无限远处的电势为零来计算。
Key-point
计算某点a的电势的可以使用从该点到无穷远的电场的积分:
\[
V = \int_{a}^{\infty} \boldsymbol{E} \cdot d\boldsymbol{l}
\]
因为\(W_{a}^{\infty}=-U_{a}^{\infty}=U_a-U_{\infty}\),而 \(U_{\infty}=0\),\(W=\int q \boldsymbol{E} \cdot d\boldsymbol{l}\),\(V = \frac{U}{q}\)
根据这个式子可以得到 点电荷产生的电势
\[
V = \frac{q}{4 \pi \varepsilon_0 r}
\]
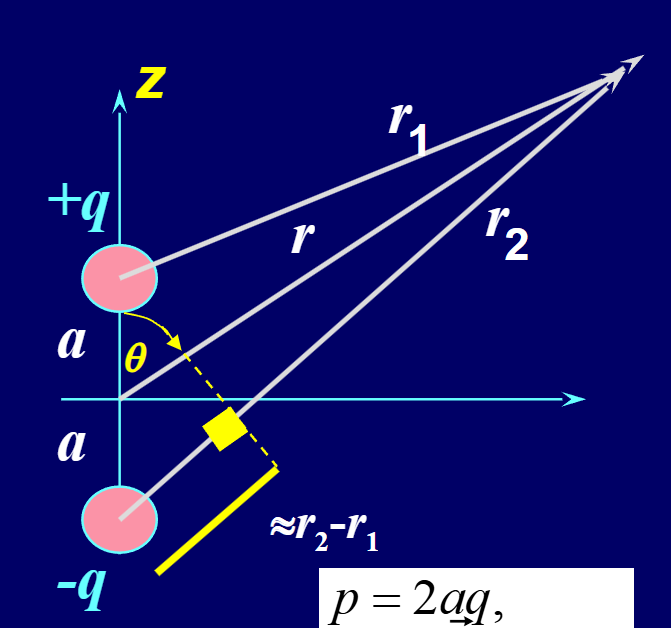
根据点电荷产生的电势,可以得到电偶极矩产生的电势
\[\begin{align*}
V &= \dfrac{q}{4 \pi \varepsilon_0} \left( \frac{1}{r_1} - \frac{1}{r_2} \right)\\
&= \dfrac{q}{4 \pi \varepsilon_0} \left( \frac{r_1-r_2}{r_1r_2}\right)
\end{align*}\]
当 \(r >> a\), \(r_1 \approx r_2 \approx r\),所以\(r_1-r_2 \approx 2a\cos \theta,r_1r_2 \approx r^2,p=2aq\)
\[\begin{align*}
V &= \dfrac{q}{4 \pi \varepsilon_0} \left( \dfrac{2a \cos \theta}{r^2}\right)\\
&= \dfrac{p \cos \theta}{4 \pi \varepsilon_0 r^2}\\
&= \dfrac{p \cdot \hat{r}}{4 \pi \varepsilon_0 r^2}
\end{align*}\]
\(\theta = \frac{\pi}{2},V=0;\theta=0,V_{max}>0;\theta=\pi,V_{min}<0\)
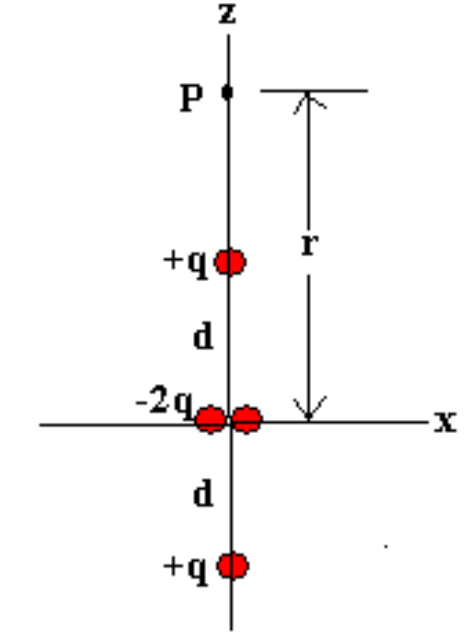
也可以推导电四偶极矩的电势
\[\begin{align*}
V(r) &= \sum_i V_i(r_i) \\
&= \frac{1}{4 \pi \epsilon_0} \left( \frac{q}{r - d} + \frac{-2q}{r} + \frac{q}{r + d} \right) \\
&= \frac{1}{4 \pi \epsilon_0} \frac{2 q d^2}{r(r^2 - d^2)} \\
&= \frac{1}{4 \pi \epsilon_0} \frac{2 q d^2}{r^3 \left( 1 - \frac{d^2}{r^2} \right)}
\end{align*}\]
\[For \enspace d << r, \frac{d^2}{r^2} << 1 \\ V(r) = \frac{2 q d^2}{4 \pi \epsilon_0 r^3} = \frac{Q}{4 \pi \epsilon_0 r^3}\]
其中 \(Q = 2qd^2\) 是电四偶极矩
Key-point
对于点电荷, \(V \propto \frac{1}{r}\), 对于电偶极矩,\(V \propto \frac{1}{r^2}\), 对于电四偶极矩,\(V \propto \frac{1}{r^3}\)
通过测量电势判断电荷的分布
$$
V\left(r\right)= \frac{1}{4 \pi \epsilon_0} \left( \frac{A_1}{r} + \frac{A_2}{r^2} + \frac{A_3}{r^3} + \dots \right) \
= \frac{1}{4 \pi \epsilon_0} \sum_i \frac{A_i}{r^i}
$$
球壳的电势
利用Guass定理,我们可以得到球壳的电场分布:
在球壳内部,电场为0,在球壳外部,电场为点电荷产生的电场
则对于距离球心距离为 \(r\) 的点,其电势有以下两种情况
- \(r < R\),则 \(V = \int_{r}^{R} E \cdot dr + \int_{R}^{+\infty} E \cdot dr = 0 + \frac{q}{4 \pi \epsilon_0 R}\)
- \(r > R\),则 \(V = \int_{r}^{+\infty}= \frac{q}{4 \pi \epsilon_0 r}\)
对于该球壳的电势能,可以将其分隔为很多个小电荷,然后对每个小电荷的电势能求和,由于\(ij\)对称性,要乘以\(\frac{1}{2}\)
\[\begin{align*}
U &= \sum_{i,j=1 (j > i)}^{n} \frac{q_i q_j}{4 \pi \varepsilon_0 r_{ij}} \\
&= \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \frac{q_i q_j}{4 \pi \varepsilon_0 r_{ij}} \\
&= \frac{1}{2} \sum_{i=1}^{n} q_i V_i \\
&= \frac{1}{2} \int V dq = \frac{1}{2} \cdot \frac{q}{4 \pi \varepsilon_0 R} \cdot q \\
&= \frac{q^2}{8 \pi \varepsilon_0 R}
\end{align*}\]
解释
固定 \(i\) ,先对 \(j\) 求和,相当于整个球壳在 \(i\) 产生的电势 \(V_i\) ,再对 \(i\) 求和,此时由于球壳内和球壳上的电势都是 \(\dfrac{q}{4 \pi \epsilon_0 R}\) ,所以最后只需要对于球壳上的电荷求和即可,通过结果我们可以发现 电势能蕴藏在电场中
估算电子的半径
电子的电势能与其原子能相等,这样处于平衡状态
\[\begin{align*}
W &= mc^2 = \frac{e^2}{8 \pi \varepsilon_0 R} \\
R &= \frac{e^2}{8 \pi \varepsilon_0 mc^2} \approx 1.4 \times 10^{-15} \ m
\end{align*}\]
圆环和圆盘的电势
圆环
圆盘
通过电势求电场
由于我们有
\[
V_{a}^{b} = -\int_{a}^{b} \boldsymbol{E} \cdot d\boldsymbol{l}
\]
故
\[
dV = -\boldsymbol{E} \cdot d\boldsymbol{l}
\]
\[
\boldsymbol{E} = - \frac{dV}{dl}= - \nabla V
\]
即求某一方向的电场,只需要求该方向的电势的偏导数即可
射影法求电场
通过电场线的类似性构造新的电荷来求电场;例如感应在无穷长的导体板上的电场,可以类似于在对称的位置上放上一个点电荷
Capacitance(电容)
Definition
电容器的电容定义为
\[
C = \frac{q}{V}
\]
其中 \(q\) 是电容器上的电荷,\(V\) 是电容器上的电势差
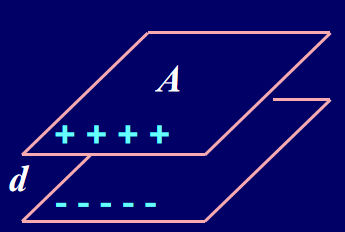
平行板电容器
\[
V=\int_{a}^{b} \boldsymbol{E} \cdot d\boldsymbol{l} = E \cdot d = \frac{\sigma}{\varepsilon_0}d
\]
\[
C = \frac{q}{V} = \dfrac{\sigma A}{\frac{\sigma}{\varepsilon_0}d}= \frac{\varepsilon_0 A}{d}
\]
故平行板电容器的电容与板的面积成正比,与板的距离成反比,即与电容器的几何参数有关
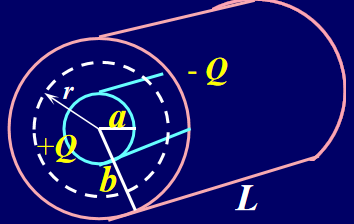
圆柱电容器
首先用高斯定律计算电场
\[
E \cdot 2 \pi r l = \frac{\lambda l}{\varepsilon_0} \Rightarrow E = \frac{\lambda}{2 \pi \varepsilon_0 r}
\]
\[
V = \int_{a}^{b} E \cdot dr = \int_{a}^{b} \frac{\lambda}{2 \pi \varepsilon_0 r} dr = \frac{\lambda}{2 \pi \varepsilon_0} \ln \frac{b}{a}
\]
\[
C = \frac{q=\lambda l}{V} = \frac{2 \pi \varepsilon_0 l}{\ln \frac{b}{a}}
\]
那么对于单位长度的电容,有
\[
C' = \frac{C}{l} = \frac{2 \pi \varepsilon_0}{\ln \frac{b}{a}}
\]
球形电容器
\[
E \cdot 4 \pi r^2 = \frac{q}{\varepsilon_0} \Rightarrow E = \frac{q}{4 \pi \varepsilon_0 r^2}
\]
\[
V = \int_{a}^{b} E \cdot dr = \int_{a}^{b} \frac{q}{4 \pi \varepsilon_0 r^2} dr = \frac{q}{4 \pi \varepsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right)
\]
\[
C = \frac{q}{V} = 4 \pi \varepsilon_0 \frac{ab}{b-a}
\]
Property
特别的,当 \(b \to \infty\) 时,\(C = 4 \pi \varepsilon_0 a\),这说明电容并不一定需要两个,一个导体也可以作为电容
电容器的并联和串联
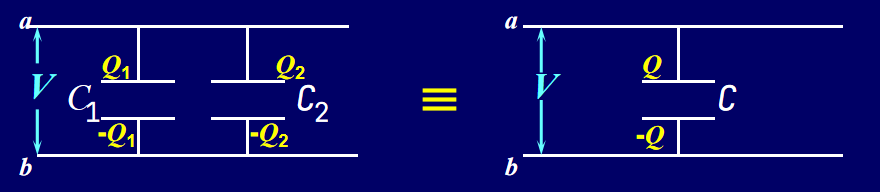
并联(电压一致)
\[
V=\frac{Q_1}{C_1}=\frac{Q_2}{C_2} \Rightarrow Q = Q_1 + Q_2 = C_1 V + C_2 V = (C_1 + C_2) V
\]
\[
C = \frac{Q}{V} = C_1 + C_2
\]
串联(电荷一致)
\[
Q = Q_1 = Q_2 = C_1 V_1 = C_2 V_2
\]
\[
V = V_1 + V_2 = \frac{Q}{C_1} + \frac{Q}{C_2} = Q \left( \frac{1}{C_1} + \frac{1}{C_2} \right)
\]
\[
C = \frac{Q}{V} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2}}
\]
\[
\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}
\]
Key-point
串联电容器的电容是并联电容器的倒数的和,而并联电容器的电容是串联电容器的和,这恰好跟电阻的串联和并联相反
电容器的能量
考虑一个平行板电容器,其电容为 \(C\),电压为 \(V\),则其具有的能量相当于从负极板不断将电荷移动到正极板,这样的过程中克服电场力所做的功
\[
U= \int_{0}^{Q} V dq = \int_{0}^{Q} \frac{q}{C} dq = \frac{Q^2}{2C} = \frac{1}{2} CV^2
\]
它的能量储存在它的电场中;由于\(V=Ed\);
\[
U = \frac{1}{2} \varepsilon_0 E^2 A d
\]
这样就得到单位体积的电场能量密度
Key-point
\[
\mu=\frac{U}{V} = \frac{1}{2} \varepsilon_0 E^2
\]
Warning
虽然公式是由平行板电容器推导出来的,但是这个公式以及能量密度公式对于任何电容器都是成立的
电介质,电场中的绝缘体
影响电容还有另外一个十分重要的因素,介电常数\(\kappa_e\),当电容器中插入电介质时,电容器的电容会增加,具体为
\[
C=C_0 \kappa_e
\]
宏观解释
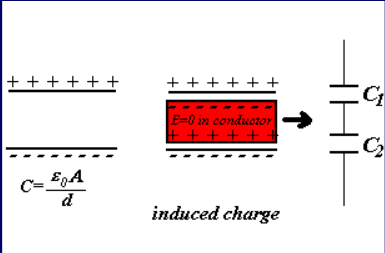
- 在平行板电容器中插入一根导体,其表面会产生感应电荷,相当于两个电容器串联
\[\begin{align*}
C_1 &= \varepsilon_0 \frac{A}{d_1} \\
C_2 &= \varepsilon_0 \frac{A}{d_2} \\
C&=\frac{C_1C_2}{C_1+C_2}=\varepsilon_0 \frac{A}{d_1+d_2}
\end{align*}\]
电容变大了,但是不能插入的导体不能太厚,否则间隙太小,很容易就达到空气的击穿电压,所以即使导体能很很好的增加电容,我们也不使用,而是使用其他的电介质
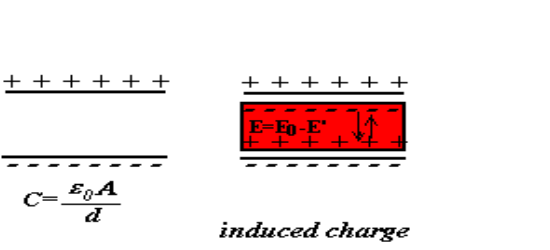
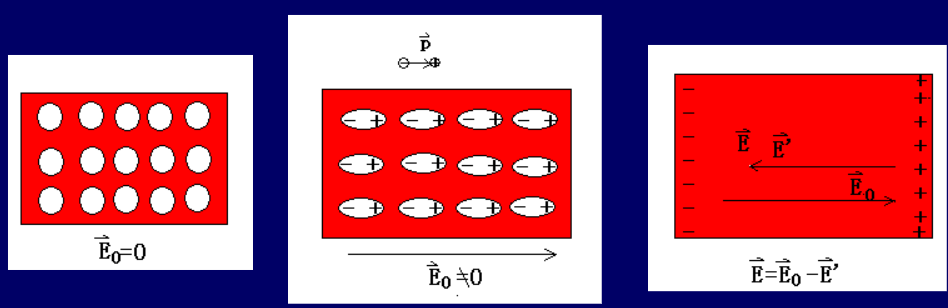
- 在平行板电容器中插入一根电介质,使其充满间隙;其表面会产生束缚电荷,在介质之间会产生感应电场,抵消掉原电场的一部分(但是不为0);两极板间的电场减小,电压减小,电荷量不变,电容增大;此时我们称该介质被极化(polarization)了
Info
其实,在英文的教材中,不管是感应电荷还是束缚电荷,都使用 induced charge 来表示,在中文中,我们为了区分导体产生的与非导体产生的,所以使用了不同的词汇
极化微观解释
Definiton
- Non-polar dielectrics:无极分子电介质,指的是分子中的正负电荷中心重合,如氧气,氮气, 二氧化碳等
- Polar dielectrics:有极分子电介质,指的是分子中的正负电荷中心不重合,如水
对于 Non-polar dielectrics,当电场作用于其上时,它会将重合的正负电荷中心分开,形成电偶极矩,这样就会产生一个与电场方向相反的电场,从而减小了电场强度(内部的电场矢量求和之后,相当于在表面分别产生正负电荷)
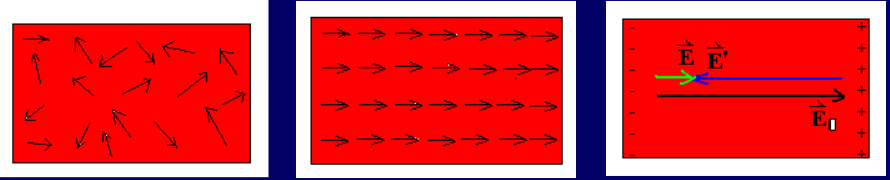
对于 Polar dielectrics,当电场作用于其上时,它会给原本杂乱无章的电偶极矩一个力矩,这个力矩会使得电偶极矩偏向电场方向,这样的极化叫做 取向极化
Note
当取向极化发生时,电子云的位移也会发生,但是彼此差了两个量级,一般忽略了电子云的位移;但是当外部电场变化频率很大时,电偶极矩转来转去是跟不上的,但是电子云的左右移动是可以的,这时候电子云的位移是主要影响的因素
极化强度矢量(Polarization)
Definition
极化强度矢量 \(\boldsymbol{P}\) 定义为单位体积内的电偶极矩之和
\[
\boldsymbol{P} = \frac{\sum \boldsymbol{p}}{\Delta V}
\]
其中 \(\boldsymbol{p}\) 是单位体积内的电偶极矩;
\(P\) 可能是均匀的,也可能是不均匀的
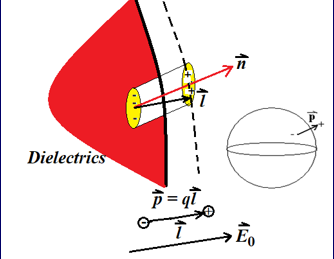
对于任意的电介质,在其表面取一个小斜圆筒,母线与电场方向一致,长度为一个电偶长度;底面与该表面的法向量垂直,这样斜斜圆筒内只可能有正电荷;
设 \(n\) 为单位体积内的电偶极矩数目(分子数目)
则
\[\begin{align*}
\boldsymbol{P} &= \frac{\sum \boldsymbol{p}}{\Delta V} = nql\\
dN&=ndV=nldA \cos \theta \\
dq'&=qdN=nql dA\cos \theta \\
&=\boldsymbol{p} \cdot \boldsymbol{dA}
\end{align*}\]
所以
\[
\oiint \boldsymbol{P} \cdot d\boldsymbol{A} = \sum_{out} q'=-\sum_{in} q'
\]
Key-point
极化强度矢量与闭合曲面的内积积分等于该曲面表面的束缚电荷,等于该曲面内部电荷的相反数(外面有多少正的,里面就有多少负的)
同时
\[
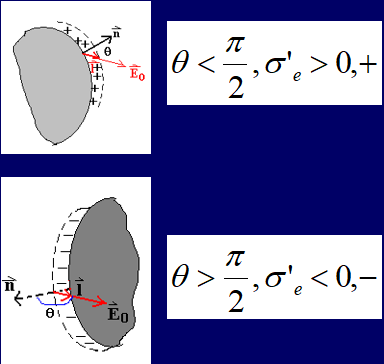
\sigma' = \dfrac{dq'}{dA} = \boldsymbol{P} \cdot \boldsymbol{n}
\]
面电荷密度等于极化强度矢量在法向上的分量;由夹角来控制正负
电介质的极化规律
Definition
在各向异性的介质中,极化强度矢量是电场的函数,在各项同性的材料中\(\boldsymbol{P}=\varepsilon_0 \chi_e E\)
其中 \(\chi_e\) 是电介质的电极化率,与介电常数的关系为 \(\kappa_e = 1 + \chi_e\)
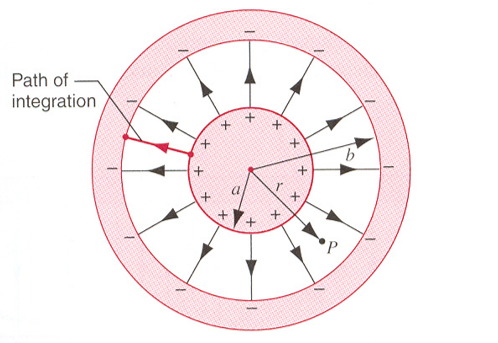
Guass定律的推广
考虑一个正电荷 \(q_0\) 放在电介质中,其周围会产生极化
由 高斯定理,我们可以得到
\[
\varepsilon_0 \oiint \boldsymbol{E} \cdot d\boldsymbol{A} = q_0 + q'
\]
\[
\oiint \boldsymbol{P} \cdot d \boldsymbol{A} = -q'
\]
\[ \varepsilon_0 \oiint \boldsymbol{E} \cdot d\boldsymbol{A} = q_0 - \oiint \boldsymbol{P} \cdot d\boldsymbol{A} \]
\[ \oiint(\varepsilon_0 \boldsymbol{E} + \boldsymbol{P}) \cdot d\boldsymbol{A} = q_0 \]
\[ \oiint \boldsymbol{D} \cdot d\boldsymbol{A} = q_0 \]
其中 \(\boldsymbol{D} = \varepsilon_0 \boldsymbol{E} + \boldsymbol{P}\) 称为电位移矢量,也叫做电感应矢量
这说明电位移矢量与闭合曲面内积面积分等于该曲面内的 自由电荷 之和
Key-point
\[
\boldsymbol{D} = \varepsilon_0 \boldsymbol{E} + \boldsymbol{P} = (1+ \chi_e)\varepsilon_0 \boldsymbol{E} =\kappa_e \varepsilon_0 \boldsymbol{E}
\]
Example
在上面的例子中
\[\begin{align*}
\oiint \vec{D} \cdot d\vec{A} &= \sum q_0 \\
4 \pi r^2 D &= q_0 \\
D &= \frac{q_0}{4 \pi r^2} \\
E &= \frac{D}{\kappa_e \varepsilon_0} = \frac{q_0}{4 \pi \varepsilon_0 \kappa_e r^2} = \frac{E_0}{\kappa_e}
\end{align*}\]
Note
\(E\)是真实电场,\(E_0\)真空中的电场
恒定电流
电流与电流密度
电流
电流定义为单位时间内通过某一横截面的电荷量
\[
I = \frac{dq}{dt}
\]
若单位体积内电荷数目为 \(n\),截面表面积为 \(s\) 电荷为 \(e\),速度为 \(v\),则电流为
\[
I = nesv
\]
电流密度
电流密度定义为单位时间内通过单位面积的电荷量
\[
\boldsymbol{J} = \frac{d\boldsymbol{I}}{d\boldsymbol{A}}
\]
其中 \(\boldsymbol{J}\) 是电流密度,\(\boldsymbol{I}\) 是电流,\(\boldsymbol{A}\) 是横截面积
有:
\[
i=\oiint \boldsymbol{J} \cdot d\boldsymbol{A}
\]
在微小变化中,有
\[
j = nev
\]
电阻与电导
电阻的定义式
\[
R = \frac{dV}{dI}
\]
电阻是决定式
\[
R = \rho \frac{l}{A} = \frac{l}{\sigma A}
\]
其中 \(\rho\) 是电阻率,\(\sigma\) 是电导率
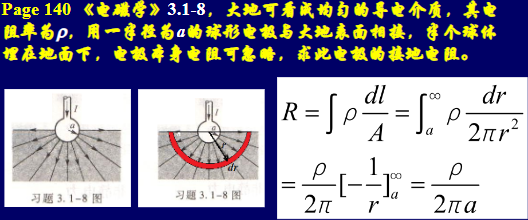
对于不规则物体,采用积分计算电阻
计算电阻
在地质勘探中,时常利用这种方法来勘探地底的资源,因为各种材料的电导率不同
欧姆定律的微分形式
\[
di = \frac{dv}{R} \quad dv= E \cdot dl
\]
\[
\boldsymbol{J} \cdot d \boldsymbol{A} = di
\]
\[
R=\rho \frac{dl}{dA}
\]
可以推出
\[
\boldsymbol{J} = \sigma \boldsymbol{E}
\]
电功率与焦耳定律
电功率
电功率定义为单位时间内电流做的功
\[
P = \frac{dW}{dt} = \frac{dW}{dq} \frac{dq}{dt} = V \cdot I
\]
其中 \(P\) 是电功率,\(W\) 是电功,\(V\) 是电压,\(I\) 是电流
焦耳定律
对于 纯电阻电路 ,电功率可以表示为\(P = I^2 R = \dfrac{V^2}{R}\)
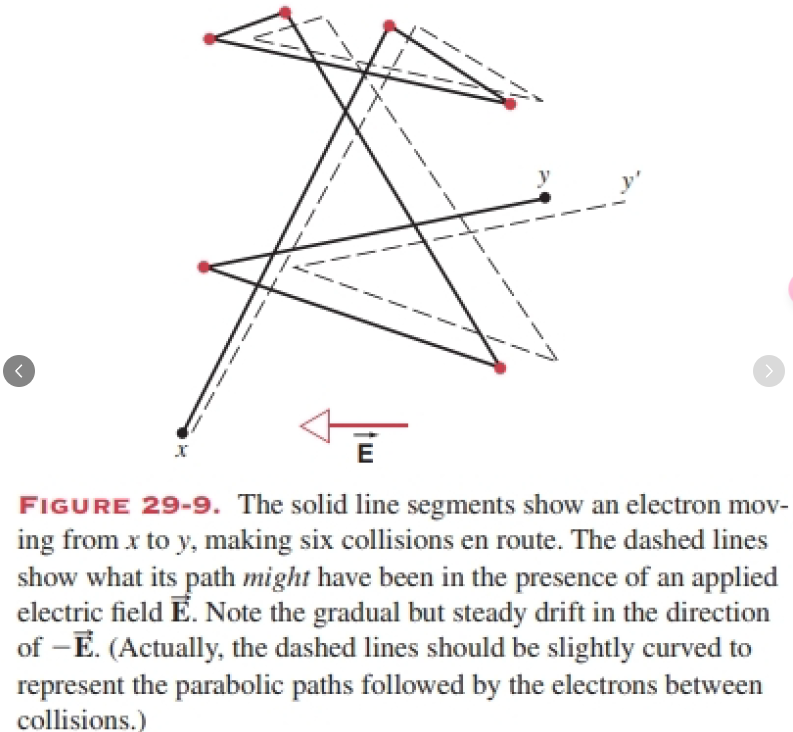
欧姆定律的微观解释
原本在导体中做热运动的电子,在施加了外部电场后,会产生漂移速度;
\[\begin{align*}
\boldsymbol{a} &= \frac{e \boldsymbol{E}}{m} \\
\overline{v} &= \frac{1}{2} \boldsymbol{a} t = \frac{e \boldsymbol{E} t}{2m} \\
&= \frac{e \boldsymbol{E} l}{2m v_d} \\
\boldsymbol{J} &= ne \overline{v} = \dfrac{n e^2 \boldsymbol{E} l}{2m v_d} = \sigma \boldsymbol{E}\\
\sigma &= \dfrac{n e^2 l}{2m v_d} \propto \frac{1}{\sqrt{T}}
\end{align*}\]
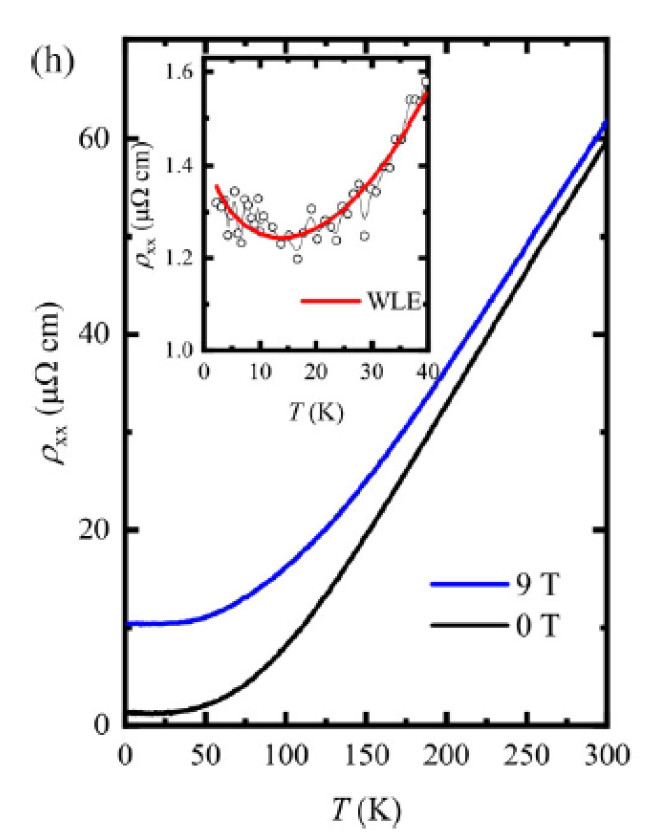
其中 \(\lambda\) 是电子的平均自由程,\(v_d\) 是电子的热运动速度,与\(\sqrt{T}\)成正比
这种算法给出了我们经典物理学中关于电阻的解释,与\(T\)是开方函数的关系,但是这只在定性方面的正确的,确实随着温度的升高,电阻会增大;但是更加现实具体的推导需要量子力学的帮助,才能给出很好的解释