磁学部分
Ampere's Law
对于电学,我们有库仑定律
\[
d \boldsymbol{F} = \frac{1}{4 \pi \epsilon_0} \frac{dq_1 dq_2}{r^2}
\]
Ampere's Law
\[
dF_{12} = \frac{\mu_0}{4 \pi} \frac{i_2 ds_2 \times (i_1ds_1 \times \hat{r_{12}})}{r_{12}^2}
\]
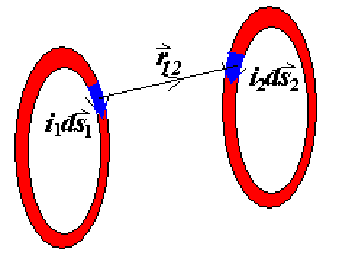
其中,\(\mu_0\) 是真空磁导率,\(i_1, i_2\) 是电流,\(ds_1, ds_2\) 是电流元长度,\(r_{12}\) 是电流元之间的距离。
Newton's Third Law
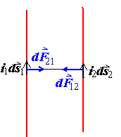
Case 1: 两电流元平行
\[
F_{12} = \frac{\mu_0}{4 \pi} \frac{i_2 ds_2 \times (i_1ds_1 \times \hat{r_{12}})}{r_{12}^2}
\]
\[
F_{21} = \frac{\mu_0}{4 \pi} \frac{i_1 ds_1 \times (i_2ds_2 \times \hat{r_{21}})}{r_{21}^2}
\]
\[
F_{12} = -F_{21}
\]
Case 2: 两电流元垂直
\[
F_{12} = 0
\]
\[
F_{21} = \frac{\mu_0}{4 \pi} \frac{i_1 ds_1 \times (i_2ds_2 \times r_{21})}{r_{21}^2} \neq 0
\]
Why?
这只是一小段的电流元,当考虑一整段电流时,得到的结果并不违背牛顿第三定律,当年安培就是利用相互垂直时的这一特性,巧妙的设计了实验来证明了安培定律。
Biot-Savart Law
继续根据电场中的思想,引入试探电流源并定义 磁感应强度
如果固定一个电流元,积分另一电流元,我们有
\[
d\boldsymbol{F}_2 = i_2 d\boldsymbol{s}_2 \times \frac{\mu_0}{4\pi} \int_{L_1} \frac{i_1 d\boldsymbol{s}_1 \times \hat{r}_{12}}{r_{12}^2}
\]
定义:
\[
\boldsymbol{B}_1 = \frac{\mu_0}{4\pi} \int_{L_1} \frac{i_1 d\boldsymbol{s}_1 \times \hat{r}_{12}}{r_{12}^2}
\]
因此:
\[
d\boldsymbol{F}_2 = i_2 d\boldsymbol{s}_2 \times \boldsymbol{B}_1
\]
磁感应强度
\[
\boldsymbol{B} = \frac{\mu_0}{4\pi} \int_{L} \frac{i d\boldsymbol{s} \times \hat{r}}{r^2}
\]
单位为 \(T\) ,特斯拉。
为什么不是磁场强度?
如果要完全跟电场对应,应该使用磁场强度,但是却叫磁感应强度,这是因为大家都这么叫
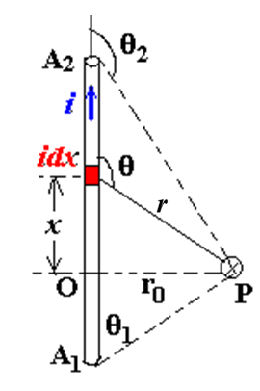
长直导线周围的磁场场
\[\begin{align*}
d\boldsymbol{B} &= \frac{\mu_0}{4\pi} \frac{i d\boldsymbol{s} \times \hat{r}}{r^2} \\
d B &= \frac{\mu_0}{4\pi} \frac{i ds \sin \theta}{r^2}\\
B &= \frac{\mu_0}{4\pi} \int_{A_1}^{A_2} \frac{i ds \sin \theta}{r^2}\\
r &= \frac{r_0}{\sin \theta}\\
s &= r_0 \cot (\pi - \theta) = -r_0 \cot \theta\\
ds &= r_0 \csc^2 \theta d\theta= r_0 \frac{d \theta}{\sin^2 \theta} \\
B &= \frac{\mu_0 i}{4\pi r_0} \int_{\theta_1}^{\theta_2} \sin \theta d\theta\\
&= \frac{\mu_0 i}{4\pi r_0} (\cos \theta_1 - \cos \theta_2)
\end{align*}\]
如果是无限长,则
\[
B = \frac{\mu_0 i}{2\pi r_0}
\]
也就是说,无限长直导线周围的磁感应强度与距离成反比。
Note
回忆电场中的无限长直导线,其电场强度与距离成反比。
\[
E = \frac{\lambda}{2\pi \epsilon_0 r}
\]
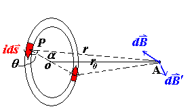
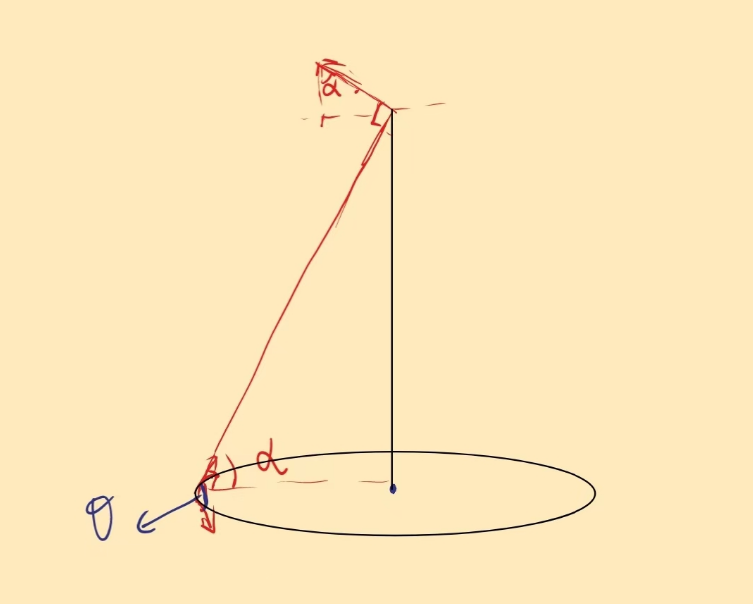
圆电流轴线上的磁场
其中由于对称性在与圆环平行的方向上,磁感应强度为零。
\[
dB = \frac{\mu_0}{4\pi} \frac{i ds \sin \theta}{r^2} = \frac{\mu_0}{4\pi} \frac{i ds}{r^2}(\theta = \frac{\pi}{2})
\]
\[
dB_x= dB \cos \alpha= \frac{\mu_0}{4 \pi} \frac{i ds}{r^2} \cos \alpha
\]
\[
r=\frac{r_0}{\sin \alpha}
\]
\[
B= \frac{\mu_0 i}{4\pi r_0^2} \int_{s} \sin^2 \alpha \cos \alpha ds =\frac{\mu_0 i}{4\pi r_0} \sin^2 \alpha \cos \alpha 2 \pi R
\]
\[
\sin \alpha = \frac{r_0}{\sqrt{r_0^2 + R^2}} \enspace \cos \alpha = \frac{R}{\sqrt{r_0^2 + R^2}}
\]
\[
B = \frac{\mu_0}{2} \frac{iR^2}{(r_0^2 + R^2)^{3/2}}
\]
Note
当 \(r_0 \to 0\) 时,\(B \to \frac{\mu_0 i}{2R}\)
当 \(r_0 \to \infty\) 时,\(B \to \frac{\mu_0 i}{2r_0^3}R^2\) 与 \(r_0^3\) 成反比。在磁场中,电偶极矩在无穷远处产生的电场也与 \(r^3\) 成反比。
定义磁偶极矩
\[
\boldsymbol{m} = i \pi R^2
\]
则
\[
B = \frac{\mu_0 i}{2r_0^3}R^2 = \frac{\mu_0 m}{2 \pi r_0^3}
\]
如果有N匝线圈,则
\[
B = \frac{\mu_0 N i}{2r_0^3}R^2 = \frac{\mu_0 N m}{2 \pi r_0^3}
\]
或者令 \(m' = N i \pi R^2\) ,
\[
B = \frac{\mu_0 m'}{2 \pi r_0^3}
\]
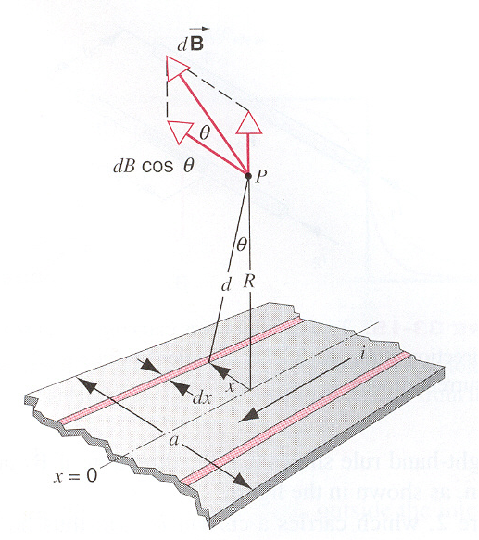
电流平面产生的磁场
由于对称性,在只会在\(x\) 方向上产生磁场
\[
dB = \frac{\mu_0 di}{2\pi d} = \frac{\mu_0 \frac{i}{a} dx}{2\pi d}
\]
\[
dB_x = dB \cdot \cos \theta
\]
\[
d = \frac{R}{\cos \theta}
\]
\[
B_x = \int dB_x = \int \frac{\mu_0 i \cos^2 \theta dx}{2\pi Ra} = \frac{\mu_0 i}{2\pi aR} \int \cos^2 \theta dx
\]
\[
x = R \tan \theta, \quad dx = \frac{R \, d\theta}{\cos^2 \theta}
\]
\[
B_x = \frac{\mu_0 i}{2\pi aR} \int \cos^2 \theta dx = \frac{\mu_0 i}{2\pi a} \int_{-\alpha}^{\alpha} d\theta = \frac{\mu_0 i}{\pi a} \alpha = \frac{\mu_0 i}{\pi a} \tan^{-1} \frac{a}{2R}
\]
Note
当 $a \to 0,\alpha \to \tan\alpha = \dfrac{a}{2R} $ 时,\(B_x \to \dfrac{\mu_0 i}{2\pi R}\)
当 \(a \to \infty, \alpha \to \dfrac{\pi}{2}\) 时, \(B_x \to \dfrac{\mu_0 i}{2 a}=\dfrac{1}{2}\mu_0 n i_0\) ,n为单位长度电流数目i_0为单位电流
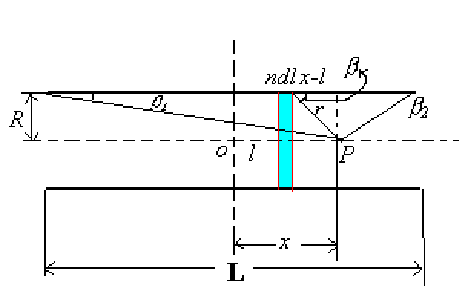
单层通电螺旋管产生的磁场
在通电螺旋管内部,会产生匀强磁场
设\(x\) 为点P据中心轴线的水平距离;螺线管长度为\(L\) ,单位长度匝数为\(n\) ,每匝电流为\(i\) 。
根据磁偶极矩产生的磁场公式
\[
dB = \dfrac{\mu_0 m}{2\pi r^3}=\dfrac{\mu_0 n i dl \pi R^2}{2\pi (\sqrt{R^2+(x-l)^2})^3}
\]
\[
r=\dfrac{R}{\sin \beta} \quad \dfrac{x-l}{R} =\cot \beta \quad dl = \dfrac{R d\beta}{\sin^2 \beta}
\]
\[
B =\frac{\mu_0}{2} n i \int_{\beta_1}^{\beta_2} \sin \beta d\beta = \frac{\mu_0}{2} n i (\cos \beta_1 - \cos \beta_2)
\]
Note
\(L \to \infty\) 时,\(B = \mu_0 n i\)
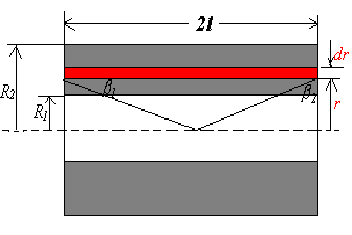
多层通电螺线管产生的磁场
从下往上,逐层积分
\[
dB=\frac{\mu_0}{2} n i (\cos \beta_1 - \cos \beta_2)
\]
\(ni\) 为每一层单位长度的电流,
\[
ni = \frac{N'i}{L} =\frac{jLdr}{L}=jdr=\frac{Ni}{L(R_2-R_1)}dr
\]
其中\(N'\) 为每一层的匝数,\(j\) 电流密度,\(R_1,R_2\) 为内外半径,\(N\) 为总匝数。
\[
\cos \beta_1 - \cos \beta_2 =2\cos \beta_1 =\dfrac{2l}{\sqrt{l^2+r^2}}
\]
\[
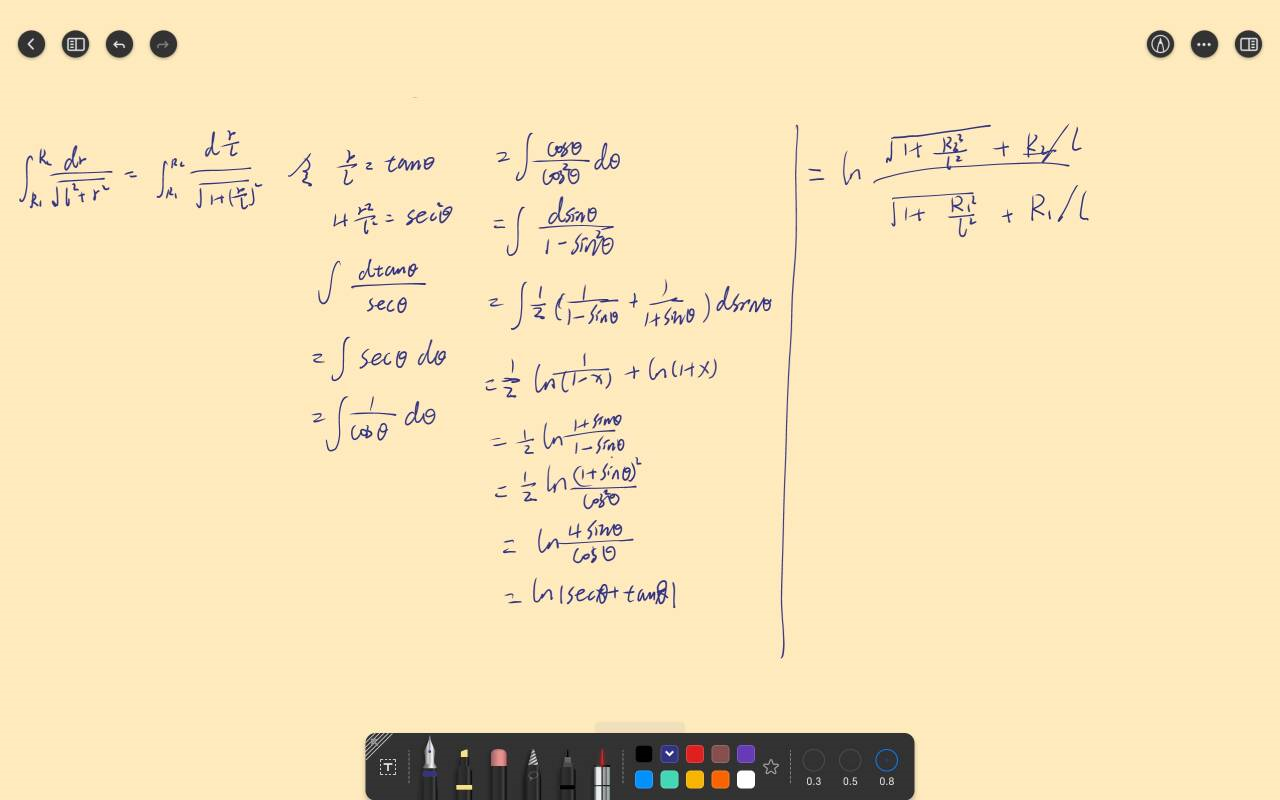
dB=\frac{\mu_0}{2} jdr \frac{2l}{\sqrt{l^2+r^2}} \quad B =\mu_0 j l \int_{R_1}^{R_2} \frac{dr}{\sqrt{r^2+l^2}}
\]
\[
B = \mu_0 j l \ln \dfrac{R_2+\sqrt{R_2^2+l^2}}{R_1+\sqrt{R_1^2+l^2}}
\]
详细过程
毁了啊,secx的原函数都记不住
磁场的Gauss定律和回路定律
磁场中的Guass定律
\[
\oiint \boldsymbol{B} \cdot d \boldsymbol{A} = 0
\]
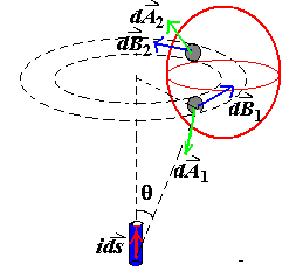
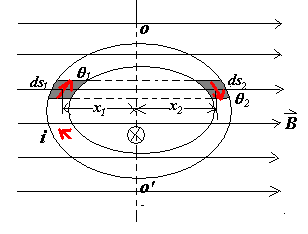
Proof
考虑在轴线处的\(ids\) 产生的磁场,对于红色的闭合曲面,可以考虑一个穿过去的小圆环;
\[
dA_1^* = |dA_1 \cos \theta_1| = dA_1 |\cos \theta_1|, \quad \theta_1 > \frac{\pi}{2}, \quad \cos \theta_1 < 0
\]
\[
dA_2^* = |dA_2 \cos \theta_2| = dA_2 |\cos \theta_2|, \quad \theta_2 < \frac{\pi}{2}, \quad \cos \theta_2 > 0
\]
\[
\therefore d\Phi_{B_1} = -d\Phi_{B_2}
\]
\[
d\Phi_{B_1} + d\Phi_{B_2} = 0
\]
\[
\oiint \vec{B} \cdot d\vec{A} = 0
\]
磁场中的回路定律
\[
\oint \boldsymbol{B} \cdot d\boldsymbol{l} =\mu_0 \sum_{in \ loop} i
\]
以右手定则判断正负,即按照积分方向使用右手定则,大拇指指向的方向就是电流的正方向,不需要对穿过去的电流进行投影,有多少穿过就直接算多少
有了回路定律,求磁场就方便得多了
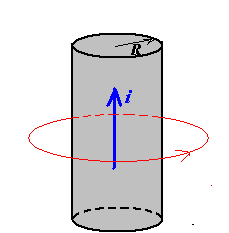
带电无穷长圆柱周围的磁场
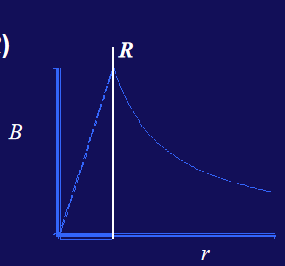
因为磁场方向与积分方向平行;半径如果是大于圆柱的半径,则
\[
B=\dfrac{\mu_0 i }{2 \pi r}
\]
如果积分区域在里面,则
\[
\oint \boldsymbol{B} \cdot d\boldsymbol{l} = \mu_0 I \dfrac{r^2}{R^2} \enspace B 2 \pi r = \mu_0 i \dfrac{r^2}{R^2}
\]
\[
B=\dfrac{\mu_0 i }{2 \pi R} \cdot \dfrac{r}{R}
\]
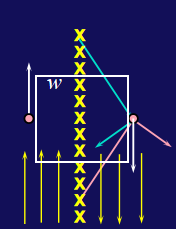
无穷大的板
因为水平方向上由于对称性,磁场为零;
在电路分布的两侧,磁场方向相反,大小相等;
设正方形的边长为\(w\) ,则
\[
\oint \boldsymbol{B} \cdot d\boldsymbol{l} = Bw + 0 + Bw + 0 = 2Bw = \mu_0 nwi
\]
\[
B=\frac{1}{2} \mu_0 n i
\]
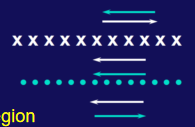
通电无穷长螺线管?为什么不是两块板
如果把螺线管中间切一刀,情况就与两块板很相似了,对于两侧,由于方向不同可以消去;
在中间,由于对称性,磁场为一块板的两倍,所以磁场为
\[
B=\mu_0 n i
\]
这正是我们之前推导的结果
螺绕环
\[
\oint \boldsymbol{B} \cdot d\boldsymbol{l} = B \cdot 2\pi r = \mu_0 Ni
\]
\[
B=\frac{1}{2} \mu_0 n i \enspace n = \frac{N}{2\pi r}
\]
电流在磁场中受到的力与力矩
\[
d\boldsymbol{F} = i d\boldsymbol{l} \times \boldsymbol{B}
\]
用右手定则来判断方向
Warning
左手定则,out!全部使用右手定则,如果是电子运动,也可以当作微小电流来处理,安培力和洛伦兹力本质上是一样的
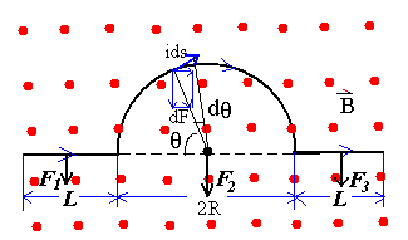
Example
平的部分很简单,弯弯的部分使用微分,发现水平部分的力由于对称性为零,只有竖直部分的力
\[
F_2 = F_\perp = \int_0^{\pi} iBR d\theta \sin \theta = iBR \int_0^{\pi} \sin \theta d\theta = 2iBR
\]
Info
安培的定义;两个相距\(1m\) 的直导线,通过的电流,产生的力为\(2 \times 10^{-7} N\) ;这样大小的电流称为\(1A\)
矩形线圈
Definition
磁偶极矩的方向为右手定则的方向
\[
\boldsymbol{\mu} = i \pi R^2 \boldsymbol{n}
\]
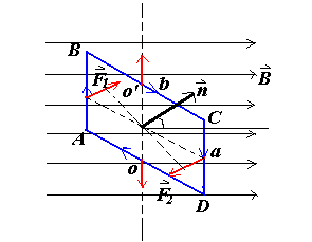
对于一个矩形线圈,如果它能绕着一个轴旋转,如图
\[
\tau = F_{AB} \frac{b}{2} \sin \theta + F_{CD} \frac{b}{2} \sin \theta
\]
\[
= i a B \frac{b}{2} \sin \theta + i a B \frac{b}{2} \sin \theta
\]
\[
= i B A \sin \theta
\]
\[
\vec{\tau} = i A (\vec{n} \times \vec{B}) = \vec{\mu} \times \vec{B}
\]
任意形状线圈
现在将结论推广到任意形状的线圈,如图,磁偶极矩与磁场垂直
将线圈分割为一个个小矩形,每个小矩形内部电流依次相消,最后合电流为原电流
\[
dF_1 = i ds_1 B \sin \theta_1
\]
\[
dF_2 = i ds_2 B \sin \theta_2
\]
\[
ds_1 \sin \theta_1 = ds_2 \sin \theta_2 = dh
\]
\[
dF_1 = dF_2 = i B dh
\]
\[
d\tau = dF_1 \cdot x_1 + dF_2 \cdot x_2
\]
\[
= iB dh (x_1 + x_2)
\]
\[
= iB dA
\]
\[
\tau = \int d\tau = \int iB dA = iBA
\]
Key-point
这种力矩使得磁偶极矩有转到磁场方向的趋势
点电荷在磁场中运动
Property
洛伦兹力不做功
洛伦兹力只改变速度方向,不改变速度大小
洛伦兹力方向用右手定则判断
对于速度为\(v\) 的点电荷,洛伦兹力为\(q \boldsymbol{v_{\perp}}\boldsymbol{B}\)
如果在匀强磁场中,做圆周运动,则\(q \boldsymbol{v_{\perp}}\boldsymbol{B} = \dfrac{mv^2}{r} \rightarrow r = \dfrac{mv}{qB}\)
速度选择器:\(\boldsymbol{E} \perp \boldsymbol{B}\) ,则\(qE = qvB \rightarrow v = \dfrac{E}{B}\) ,速度选择器接着一个磁场,根据半径不同,可以做到分离同位素
回旋加速器: 电场加速,磁场偏转,交流电的周期与粒子做圆周运动的周期相同;\(v=\dfrac{qBr}{m}\) ,\(T=\dfrac{2\pi m}{qB}\) ,\(E_k = \dfrac{1}{2}mv^2 = \dfrac{q^2 B^2 r^2}{2m}\)
Warning
当回旋加速器中的粒子速度接近光速时,粒子质量会发生变化,导致粒子做圆周运动的周期发生变化,从而导致固定的交流电频率无法一直加速;粒子无法被加速到更高的能量。可以通过修改磁场大小:
\[
m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}
\]
\[
T=\frac{2\pi m}{qB}=\frac{2\pi m_0}{qB\sqrt{1-\frac{v^2}{c^2}}}
\]
修改B;
\[
B \sqrt{1-\frac{v^2}{c^2}} = const
\]
同步加速器
霍尔效应:带电粒子在磁场中运动,在垂直于磁场方向的导体中,由于洛伦兹力,电荷会向一侧偏转,从而在导体两侧形成电势差,平衡时,洛伦兹力等于电场力,\(qE = qvB \rightarrow E = vB\) ,\(U = E \cdot d = vBd\) ,\(I = j \cdot d \cdot w = nqv \cdot d \cdot w\) ,\(j = nqv\) ,\(U = \dfrac{I B d}{nqwd}\) ,\(R_H = \dfrac{U}{I} = \dfrac{B}{nqw}\) ,\(R_H\) 称为霍尔系数,\(n\) 为载流子浓度,\(q\) 为载流子电量,\(w\) 为导体宽度,\(d\) 为导体厚度